题目内容
8. 如图,长方形宽AB=5cm,长BC=13cm,现将长方形折叠,使顶点D落在BC边上的点F处(折痕为AE),则EF=2.6cm.
如图,长方形宽AB=5cm,长BC=13cm,现将长方形折叠,使顶点D落在BC边上的点F处(折痕为AE),则EF=2.6cm.
分析 首先根据勾股定理求出BF的长,进而求出FC的长;再次根据勾股定理,列出关于线段EF的方程,求出EF的长度.
解答 解:∵四边形ABCD为矩形,
∴∠B=90°,AD=BC=13cm;DC=AB=5cm;
由题意得:AF=AD=13cm,
设EF=ED=x,
则EC=8-x;
由勾股定理得:
BF2=132-52=144,
∴BF=12,CF=13-12=1;
由勾股定理得:
x2=12+(5-x)2,
解得:x=2.6,
即EF=2.6cm,
故答案为:2.6cm.
点评 本题主要考查了翻折变换及其性质的应用问题;根据折叠的性质和勾股定理列出方程是解决问题的关键.

练习册系列答案
相关题目
19.下列等式成立的是( )
| A. | (-a3)6=a18 | B. | $\sqrt{a+b}=\sqrt{a}+\sqrt{b}$ | C. | a2•a5=a10 | D. | $\sqrt{{a}^{2}}=a$ |
17.方程5-x=3的解是( )
| A. | x=2 | B. | x=-2 | C. | x=1 | D. | x=-1 |
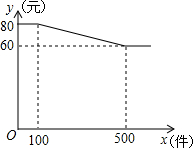 某服装厂A装,其单价y(元)与批发数量x(件)(x为正整数)之间的函
某服装厂A装,其单价y(元)与批发数量x(件)(x为正整数)之间的函