题目内容
10.观察下面一列数,按某种规律填上适当的数:(1)0、3、8、15、24、35、48;
(2)$\frac{1}{2}$、-$\frac{2}{4}$、$\frac{3}{8}$、-$\frac{4}{16}$、$\frac{5}{32}$、-$\frac{6}{64}$,$\frac{7}{128}$.
分析 (1)观察不难发现,该列数字为连续自然数的平方减1的数,然后解答即可;
(2)根据分子即为这个数,分母是2的指数次幂,并且第奇数个分数是正数,第偶数个分数是负数填写即可.
解答 解:(1)∵0=12-1,
3=22-1,
8=32-1,
15=42-1,
24=52-1,
…,
∴第n个数是n2-1,
∴第六个数:35,
第七个数:48;
故答案为:35,48;
(2)$\frac{1}{2}$、-$\frac{2}{4}$、$\frac{3}{8}$、-$\frac{4}{16}$、$\frac{5}{32}$、-$\frac{6}{64}$,$\frac{7}{128}$.
故答案为:-$\frac{6}{64}$,$\frac{7}{128}$.
点评 本题是对数字变化规律的考查,比较简单,关键在于从相邻两数的差和2的指数次幂考虑求解.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
1.数轴上一点对应的有理数为-7$\frac{1}{2}$,这个点在数轴上的( )
| A. | -6与-7之间 | B. | -7与-8之间 | C. | 7与8之间 | D. | 6与7之间 |
2.计算-2-1的结果是( )
| A. | -3 | B. | -2 | C. | -1 | D. | 2 |
19.下列等式成立的是( )
| A. | (-a3)6=a18 | B. | $\sqrt{a+b}=\sqrt{a}+\sqrt{b}$ | C. | a2•a5=a10 | D. | $\sqrt{{a}^{2}}=a$ |
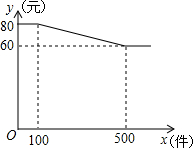 某服装厂A装,其单价y(元)与批发数量x(件)(x为正整数)之间的函
某服装厂A装,其单价y(元)与批发数量x(件)(x为正整数)之间的函