题目内容
7.某学校新建阶梯教室,第一排有25个座位,后面每排都比前一排多一个座位,若第n排有m个座位,教室共有p个座位.(1)写出m与n,p与n之间的函数式;
(2)若教室座位共有15排,座位总数将达到多少个?
分析 (1)利用第一排有25个座位,第n排的座位数为25+(n-1),相邻两排相差1,根据等差数列求和得出答案即可;
(2)把n=15代入(1)得出答案即可.
解答 解:(1)∵第一排有25=24+1个座位,后面每排都比前一排多一个座位,第n排有m个座位,
∴m与n之间的函数式为:m=24+n;
p与n之间的函数式为:
p=25+26+…+m
=(24+1)+(24+2)+(24+3)+…+(24+n)
=24n+(1+2+3+…+n)
=24n+$\frac{(1+n)n}{2}$;
(2)由(1)得:p=24×15+$\frac{(1+15)×15}{2}$=480.
点评 此题考查了列函数关系式,理解题意,找出蕴含的数量关系,列出式子解决问题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
17.下列说法,正确的是( )
| A. | 若-2+x是一个正数,则x一定是正数 | |
| B. | -a表示一个负数 | |
| C. | 如果两个数的和为零,那么这两个数一定是一正一负 | |
| D. | 两个有理数的和一定大于其中一个加数 |
18.在方程$\frac{2}{3}$x+1=$\frac{1}{2}$的两边同时乘以6,得( )
| A. | 4x+1=3 | B. | 2x+6=3 | C. | 4x+3=3 | D. | 4x+6=3 |
2.下面几个数中,是正整数的为( )
| A. | 3 | B. | -$\frac{1}{2}$ | C. | -$\sqrt{2}$ | D. | 0 |
19.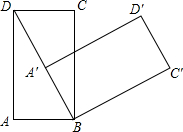 如图,矩形ABCD中,AB=1,AD=$\sqrt{3}$,若矩形ABCD以B为中心,按顺时针方向旋转到A′B′C′D′的位置(点A′落在对角线BD上),则对角线BD扫过的图形的面积为( )
如图,矩形ABCD中,AB=1,AD=$\sqrt{3}$,若矩形ABCD以B为中心,按顺时针方向旋转到A′B′C′D′的位置(点A′落在对角线BD上),则对角线BD扫过的图形的面积为( )
 如图,矩形ABCD中,AB=1,AD=$\sqrt{3}$,若矩形ABCD以B为中心,按顺时针方向旋转到A′B′C′D′的位置(点A′落在对角线BD上),则对角线BD扫过的图形的面积为( )
如图,矩形ABCD中,AB=1,AD=$\sqrt{3}$,若矩形ABCD以B为中心,按顺时针方向旋转到A′B′C′D′的位置(点A′落在对角线BD上),则对角线BD扫过的图形的面积为( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | π | D. | $\frac{4π}{3}$ |
 如图,AB=AC=5,BC=8,∠DAC=90°,则BD的长为$\frac{7}{4}$,AD=$\frac{15}{4}$.
如图,AB=AC=5,BC=8,∠DAC=90°,则BD的长为$\frac{7}{4}$,AD=$\frac{15}{4}$. 已知:如图所示,△ACF≌△DBE.将下面的推理过程补充完整.
已知:如图所示,△ACF≌△DBE.将下面的推理过程补充完整.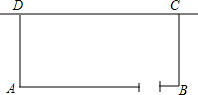 现有长28米的网,围成一个一面靠墙的矩形鸡舍:已知墙长14米,AB边可开一个或两个1米宽的门.
现有长28米的网,围成一个一面靠墙的矩形鸡舍:已知墙长14米,AB边可开一个或两个1米宽的门.