题目内容
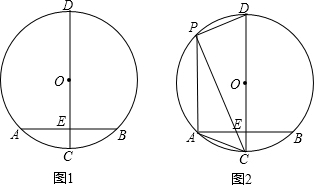
如图,A、B为⊙O上两点,直径CD平分AB,交AB于E,如图1.
(1)若AB=8,CE=2,求⊙O的半径长;
(2)如图2,P为圆上异于A、B、C、D的一点,连接PA、PB、PC、PD.若∠BAC=15°,求∠APC、∠APD和∠OBE度数.
(1)若AB=8,CE=2,求⊙O的半径长;
(2)如图2,P为圆上异于A、B、C、D的一点,连接PA、PB、PC、PD.若∠BAC=15°,求∠APC、∠APD和∠OBE度数.

考点:垂径定理,圆周角定理
专题:
分析:(1)连接OA,根据垂径定理可得出AE的长,设OA=x,则OE=OC-EC=x-2,在Rt△OAE中根据勾股定理即可得出结论;
(2)先根据垂径定理得出
=
,故可得出∠APC=∠BAC=15°,即
=15°,根据圆心角、弧、弦的关系得出∠APD的度数,再由直角三角形的性质即可得出结论.
(2)先根据垂径定理得出
 |
| AC |
 |
| BC |
 |
| AC |
解答: 解:(1)连接OA.
解:(1)连接OA.
∵直径CD平分AB,
∴CD⊥AB,AE=
AB=4,
设OA=x,则OE=OC-EC=x-2.
在Rt△OAE中,OE2+AE2=OA2,即(x-2)2+42=x2,解得x=5,
∴⊙O的半径长为5.
(2)∵直径CD平分AB,交AB于E,
∴
=
,
∴∠APC=∠BAC=15°,
∴
=15°,
∴
=90°+15°=105°,
∵∠APD=105°.
∵∠BAC=15°,
∴∠BOC=30°.
∵CD⊥AB,
∴∠OBE=90°-30°=60°.
 解:(1)连接OA.
解:(1)连接OA.∵直径CD平分AB,
∴CD⊥AB,AE=
| 1 |
| 2 |
设OA=x,则OE=OC-EC=x-2.
在Rt△OAE中,OE2+AE2=OA2,即(x-2)2+42=x2,解得x=5,
∴⊙O的半径长为5.
(2)∵直径CD平分AB,交AB于E,
∴
 |
| AC |
 |
| BC |
∴∠APC=∠BAC=15°,
∴
 |
| AC |
∴
 |
| ABD |
∵∠APD=105°.
∵∠BAC=15°,
∴∠BOC=30°.
∵CD⊥AB,
∴∠OBE=90°-30°=60°.
点评:本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
相关题目
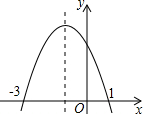 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象答下列问题: 有一圆柱,在圆柱下底的A点处有一只蚂蚁,它想吃到上底面与A点相对的B点处的食物,沿圆柱侧面爬行,如圆柱高为1dm,底面圆半径为2dm,则爬行的最短路程是
有一圆柱,在圆柱下底的A点处有一只蚂蚁,它想吃到上底面与A点相对的B点处的食物,沿圆柱侧面爬行,如圆柱高为1dm,底面圆半径为2dm,则爬行的最短路程是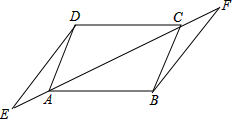 如图,AD∥BC,AE=CF,AD=BC,点E,F在直线AC上,试猜想线段DE与BF有何关系,并说明你的猜想.
如图,AD∥BC,AE=CF,AD=BC,点E,F在直线AC上,试猜想线段DE与BF有何关系,并说明你的猜想.