��Ŀ����
18�� �ҹ�����������ѧ���ؾ���������������������¡�һ���У��������������ؾ��ع�ʽ��Ҳ����б�����ʽ�������һ�������ε����߳��ֱ�Ϊa��b��c����������ε����ΪS=$\sqrt{\frac{1}{4}[{a}^{2}{b}^{2}-��\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2}��^{2}]}$������֪��ABC�����߳��ֱ�Ϊ1��2��$\sqrt{5}$�����ABC�����Ϊ1��
�ҹ�����������ѧ���ؾ���������������������¡�һ���У��������������ؾ��ع�ʽ��Ҳ����б�����ʽ�������һ�������ε����߳��ֱ�Ϊa��b��c����������ε����ΪS=$\sqrt{\frac{1}{4}[{a}^{2}{b}^{2}-��\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2}��^{2}]}$������֪��ABC�����߳��ֱ�Ϊ1��2��$\sqrt{5}$�����ABC�����Ϊ1��
���� ������Ŀ�е������ʽ������á�ABC�����߳��ֱ�Ϊ1��2��$\sqrt{5}$��������Ӷ����Խ���⣮
��� �⣺��S=$\sqrt{\frac{1}{4}[{a}^{2}{b}^{2}-��\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2}��^{2}]}$��
���ABC�����߳��ֱ�Ϊ1��2��$\sqrt{5}$�����ABC�����Ϊ��
S=$\sqrt{\frac{1}{4}[{1}^{2}��{2}^{2}-��\frac{{1}^{2}+{2}^{2}-��\sqrt{5}��^{2}}{2}��^{2}]}$=1��
�ʴ�Ϊ��1��
���� ���⿼����θ�ʽ��Ӧ�ã������Ĺؼ�����ȷ���⣬������Ŀ�е������ʽ���

��ϰ��ϵ�д�
 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
�����Ŀ
8���й��˺���Ϳ�ʼʹ�ø������й��Ŵ���ѧ�����������������ġ����̡�һ�£���������ѧʷ���״���ʽ���븺�������ӯ��100Ԫ����+100����-80Ԫ��ʾ��������
| A�� | ����20Ԫ | B�� | ӯ��20Ԫ | C�� | ����80Ԫ | D�� | ӯ��80Ԫ |
9����֪����ʽ��$\left\{\begin{array}{l}{1-3��x-1����8-x}\\{\frac{2x-5}{3}-x��-3}\end{array}\right.$����С������Ϊa�����������Ϊb����ba=��������
| A�� | $\frac{1}{9}$ | B�� | -8 | C�� | $\frac{1}{16}$ | D�� | 16 |
6��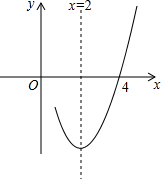 ��֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=2����x���һ����������Ϊ��4��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ�
��֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=2����x���һ����������Ϊ��4��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ�
�������߹�ԭ�㣻
��4a+b+c=0��
��a-b+c��0��
�������ߵĶ�������Ϊ��2��b����
�ݵ�x��2ʱ��y��x���������
���н�����ȷ���ǣ�������
 ��֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=2����x���һ����������Ϊ��4��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ�
��֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=2����x���һ����������Ϊ��4��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ��������߹�ԭ�㣻
��4a+b+c=0��
��a-b+c��0��
�������ߵĶ�������Ϊ��2��b����
�ݵ�x��2ʱ��y��x���������
���н�����ȷ���ǣ�������
| A�� | �٢ڢ� | B�� | �ۢܢ� | C�� | �٢ڢ� | D�� | �٢ܢ� |
10������106����102��3��104�Ľ���ǣ�������
| A�� | 103 | B�� | 107 | C�� | 108 | D�� | 109 |
7���������⡰��a2��b2����a��b���������������a��b��ֵ�У���˵����������Ǽ�������ǣ�������
| A�� | a=3��b=2 | B�� | a=-3��b=2 | C�� | a=3��b=-1 | D�� | a=-1��b=3 |

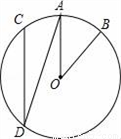
 ����AOB=40�㣬���ADC�Ķ����� _______��
����AOB=40�㣬���ADC�Ķ����� _______��