题目内容
9.已知不等式组$\left\{\begin{array}{l}{1-3(x-1)≤8-x}\\{\frac{2x-5}{3}-x>-3}\end{array}\right.$的最小整数解为a,最大整数解为b,则ba=( )| A. | $\frac{1}{9}$ | B. | -8 | C. | $\frac{1}{16}$ | D. | 16 |
分析 先求出不等式组中每个不等式的解集,然后求出其公共解集,最后求其最小整数和最大整数解即可.
解答 解:$\left\{\begin{array}{l}{1-3(x-1)≤8-x①}\\{\frac{2x-5}{3}-x>-3②}\end{array}\right.$
由①得x≥-2;
由②得x<4;
不等式组的解集为-2≤x<4;
所以a=-2,b=3.
所以ba=3-2=$\frac{1}{9}$
故选A.
点评 考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
19.下列计算结果正确的是( )
| A. | a3+a3=a6 | B. | a3•a2=a6 | C. | (a3)3=a9 | D. | a6÷a2=a3 |
20.2017年4月6日,交通运输部科学研究院对外发布《2017年第一季度中国主要城市骑行报告》,报告显示,在车均使用次数方面,昆明排名第一,成为“最爱骑共享单车的城市”.目前已经投入昆明的共享单车约有112000辆.将“112000”用科学记数法表示为( )
| A. | 1.12×103 | B. | 1.12×104 | C. | 1.12×105 | D. | 11.2×104 |
17. 如图,已知矩形ABCD,则下列结论一定正确的是( )
如图,已知矩形ABCD,则下列结论一定正确的是( )
 如图,已知矩形ABCD,则下列结论一定正确的是( )
如图,已知矩形ABCD,则下列结论一定正确的是( )| A. | ∠CAD=∠CAB | B. | OA=OD | ||
| C. | OA=AB | D. | AC所在直线为对称轴 |
14.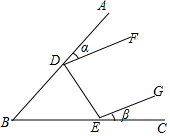 如图所示,点D,E分别在BA,BC上,∠ADF=α度,∠CEG=β度,∠ABC=γ度,DF∥EG,则( )
如图所示,点D,E分别在BA,BC上,∠ADF=α度,∠CEG=β度,∠ABC=γ度,DF∥EG,则( )
 如图所示,点D,E分别在BA,BC上,∠ADF=α度,∠CEG=β度,∠ABC=γ度,DF∥EG,则( )
如图所示,点D,E分别在BA,BC上,∠ADF=α度,∠CEG=β度,∠ABC=γ度,DF∥EG,则( )| A. | α+β+γ=180 | B. | α+β=γ | C. | α+β+γ=90 | D. | 2α+2β-γ=45 |
19.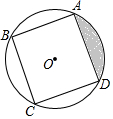 如图,正方形ABCD内接于半径为2的⊙O,则图中阴影部分的面积为( )
如图,正方形ABCD内接于半径为2的⊙O,则图中阴影部分的面积为( )
 如图,正方形ABCD内接于半径为2的⊙O,则图中阴影部分的面积为( )
如图,正方形ABCD内接于半径为2的⊙O,则图中阴影部分的面积为( )| A. | π+1 | B. | π+2 | C. | π-1 | D. | π-2 |
 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为S=$\sqrt{\frac{1}{4}[{a}^{2}{b}^{2}-(\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2})^{2}]}$.现已知△ABC的三边长分别为1,2,$\sqrt{5}$,则△ABC的面积为1.
我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为S=$\sqrt{\frac{1}{4}[{a}^{2}{b}^{2}-(\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2})^{2}]}$.现已知△ABC的三边长分别为1,2,$\sqrt{5}$,则△ABC的面积为1.