题目内容
16．
观察右面由“※”组成的图案和算式．解答问题．1+3=4=22；
1+3+5=9=32；
1+3+5+7=16=42；
1+3+5+7+9=25=52．
（1）请猜想：1+3+5+7+9+…+19=102：
（2）请猜想：1+3+5+7+9+…+（2n-1）=n2；
（3）请用上述规律计算：103+105+107+…+2013+2015．
分析 （1）（2）个数是从1开始的连续的奇数个※正好组成一个正方形，即从1开始的连续的奇数的和是一个完全平方数，是奇数的个数的平方，由此规律得出答案即可；
（3）把103+105+107+…+2013+2015=（1+3+…+101+103+105+107+…+2013+2015）-（1+3+…+101），利用上面的规律计算即可．
解答 解：1）1+3+5+7+9+…+19=102：
（2）1+3+5+7+9+…+（2n-1）=n2；
（3）103+105+107+…+2013+2015
=（1+3+…+101+103+105+107+…+2013+2015）-（1+3+…+101）
=10082-512
=1013463．
点评 此题考查数字的变化规律，找出数字之间的运算规律，利用规律解决问题．
练习册系列答案
相关题目
如图所示，利用面积的不同表示方法可证明（a+b）（a-b）=a2-b2，你能说明其中的道理吗？
为了改善小区环境，某小区决定要在一块一边靠墙（墙足够长）的空地上修建一个矩形绿化带ABCD，绿化带一边靠墙，另三边用总长为40m的栅栏围住（如图）．若设绿化带的BC边长为xm，绿化带的面积为ym2．则y与x之间的函数关系式是y=-$\frac{1}{2}$x2+20x．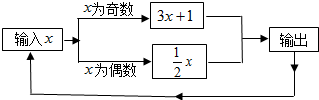
有一个数值转换器，原理如图所示，若开始输入x的值是5，可发现第1次输出的结果是16，第2次输出的结果是8，第3次输出的结果是4，依次继续下去…，第2015次输出的结果是1．
如图，四边形ABCD和EFGC都是正方形，写出表示阴影部分面积的代数式．
用代数式表示图中阴影部分的面积S=（π-2）a2．