题目内容
2. 如图,圆柱底面圆的半径为$\frac{2}{π}$ cm,高为9cm,点A,B分别是圆柱两底面圆周上的点,且A,B在同一母线上,用一根棉线从点A顺着圆柱侧面绕3圈到点B,那么这根棉线的长度最短是多少?
如图,圆柱底面圆的半径为$\frac{2}{π}$ cm,高为9cm,点A,B分别是圆柱两底面圆周上的点,且A,B在同一母线上,用一根棉线从点A顺着圆柱侧面绕3圈到点B,那么这根棉线的长度最短是多少?
分析 求圆柱体中两点之间的最短路径,最直接的作法,就是将圆柱体展开,然后利用两点之间线段最短解答.
解答  解:圆柱体的展开图如图所示,
解:圆柱体的展开图如图所示,
用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:AC→CD→DB,
即在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A沿着3个长方形的对角线运动到B的路线最短,
∵圆柱底面半径为$\frac{2}{π}$cm,
∴长方形的宽即是圆柱体的底面周长=2π×$\frac{2}{π}$=4cm,
又∵圆柱高为9cm,
∴小长方形的一条边长是3cm,
根据勾股定理求得AC=CD=DB=5cm,
∴AC+CD+DB=15cm,
答:这根棉线的长度最短是15cm.
点评 本题主要考查了圆柱的计算、平面展开-路径最短问题.圆柱的侧面展开图是一个长方形,此长方形的宽等于圆柱底面周长,长方形的长等于圆柱的高.解题的关键就是把圆柱的侧面展开成长方形,“化曲面为平面”,用勾股定理解决.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
15.某校为了了解八年级学生身高情况,在全校范围内随机抽取了若干名学生进行调查,得到的数据如表:
(1)把身高按照150-155,155-160,160-165,165-170分组,数据包括右端点不包括左端点,写出众数所在的范围?
(2)请估计该校八年级学生的平均身高(精确到1cm)?
(3)请估计该校八年级学生的中等身高是多少cm?
(4)如果选出该校八年级学生中身高在155cm-160cm共60人组建体操表演队,则该队学生身高的波动水平(方差)是多少?
| 身高(cm) | 152 | 154 | 156 | 160 | 164 | 168 | 170 |
| 频数 | 1 | 1 | 2 | 6 | 4 | 4 | 2 |
(2)请估计该校八年级学生的平均身高(精确到1cm)?
(3)请估计该校八年级学生的中等身高是多少cm?
(4)如果选出该校八年级学生中身高在155cm-160cm共60人组建体操表演队,则该队学生身高的波动水平(方差)是多少?
14.两个有理数a与b,a+b=0,a与b的关系是( )
| A. | 一正一负 | B. | 互为倒数 | C. | 互为相反数 | D. | 都是零 |
 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)…,如果(1,0)是第一个点,探究规律如下:
如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)…,如果(1,0)是第一个点,探究规律如下: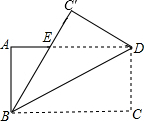 如图,矩形ABCD的长为8,宽为6,现将矩形沿对角线BD折叠,C点到达C′处,C′B交AD于E.
如图,矩形ABCD的长为8,宽为6,现将矩形沿对角线BD折叠,C点到达C′处,C′B交AD于E. 已知二次函数y=x2-2x-3
已知二次函数y=x2-2x-3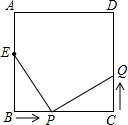 如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.如果点P在线段BC上以2cm/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动,设运动的时间为t秒,
如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.如果点P在线段BC上以2cm/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动,设运动的时间为t秒,