题目内容
10.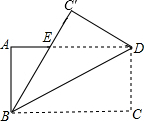 如图,矩形ABCD的长为8,宽为6,现将矩形沿对角线BD折叠,C点到达C′处,C′B交AD于E.
如图,矩形ABCD的长为8,宽为6,现将矩形沿对角线BD折叠,C点到达C′处,C′B交AD于E.(1)判断△EBD的形状,并说明理由;
(2)求DE的长.
分析 (1)因为折叠前后∠DBC=∠DBC1,且平行,内错角相等,所以∠DCB=∠DAB,所以根据角之间的等量代换可得∠C1BD=∠EDB,根据等边对等角可知DE=BE;
(2)设DE=x,则AE=AD-DE=8-x,在Rt△ABE中,根据勾股定理得:BE2=AB2+AE2,然后代入各值求解即可.
解答 (1)证明:∵△BDC1是由△BDC沿直线BD折叠得到的,
∴∠C1BD=∠CBD,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CBD=∠EDB,
∴∠C1BD=∠EDB,
∴BE=DE,
∴△EBD是等腰三角形;
(2)解:设DE=x,则AE=AD-DE=8-x,
∵∠A=90°,BE=DE=x,
在Rt△ABE中,BE2=AB2+AE2,
∴x2=62+(8-x)2,
∴x=$\frac{25}{4}$,
即DE=$\frac{25}{4}$.
点评 本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后对应线段、角相等.

练习册系列答案
相关题目
3.若-6xayzb与9x3ycz2是同类项,则a、b、c的值分别是( )
| A. | a=1 b=2 c=3 | B. | a=3 b=1 c=2 | C. | a=3 b=2 c=1 | D. | 以上都不对 |
4.为了解某小区居民六月份用水量的情况,物业办随机抽查了该小区23户家庭本月的用水量,结果如表,则这23户家庭六月份用水量的众数和中位数分别为( )
| 每户用水量(吨) | 4 | 5 | 7 | 9 | 10 | 12 |
| 户数(户) | 2 | 1 | 8 | 2 | 7 | 3 |
| A. | 100吨,7吨 | B. | 7吨,8吨 | C. | 7吨,9吨 | D. | 12吨,8吨 |
19.若3xm-n-2ym+n-2=4是关于x,y的二元一次方程,则m,n的值分别为( )
| A. | m=1,n=0 | B. | m=0,n=-1 | C. | m=2,n=1 | D. | m=2,n=-3 |
 如图是一个长方体盒子(尺寸如图所示),在长方体下底部的A点有一只蚂蚁,它想吃到上底面B点的食物(BC=3cm),需爬行的最短路程是多少?
如图是一个长方体盒子(尺寸如图所示),在长方体下底部的A点有一只蚂蚁,它想吃到上底面B点的食物(BC=3cm),需爬行的最短路程是多少? 如图所示是一张裁剪好的铁皮,利用这张铁皮可以折叠成一个立体图形.
如图所示是一张裁剪好的铁皮,利用这张铁皮可以折叠成一个立体图形. 如图,圆柱底面圆的半径为$\frac{2}{π}$ cm,高为9cm,点A,B分别是圆柱两底面圆周上的点,且A,B在同一母线上,用一根棉线从点A顺着圆柱侧面绕3圈到点B,那么这根棉线的长度最短是多少?
如图,圆柱底面圆的半径为$\frac{2}{π}$ cm,高为9cm,点A,B分别是圆柱两底面圆周上的点,且A,B在同一母线上,用一根棉线从点A顺着圆柱侧面绕3圈到点B,那么这根棉线的长度最短是多少?