题目内容
4.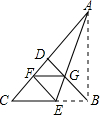 如图,在等腰直角三角形ABC中,∠ABC=90°,D是AC上的中点,E是BC上一点,将△ABC沿AE折叠,点B恰好落在边AC上的点F处,连接BD,交AE于点G,连接FG.以下结论:①tan∠EAF=$\frac{1}{2}$;②FG∥BC;③点E关于FG对称的点不在边AC上;④BE=BG;⑤S四边形DFEG=S△ADG其中正确的有( )
如图,在等腰直角三角形ABC中,∠ABC=90°,D是AC上的中点,E是BC上一点,将△ABC沿AE折叠,点B恰好落在边AC上的点F处,连接BD,交AE于点G,连接FG.以下结论:①tan∠EAF=$\frac{1}{2}$;②FG∥BC;③点E关于FG对称的点不在边AC上;④BE=BG;⑤S四边形DFEG=S△ADG其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①错误,设EB=EF=FC=a,则EC=$\sqrt{2}$a,AB=BC=($\sqrt{2}$+1)a,因为∠EAB=∠EAF,求出tan∠EAB即可.②正确,只要证明FG是∠AFE角平分线即可.③错误.可以根据∠AFG=∠EFG进行判断.④正确,只要证明四边形EFGB是菱形即可,⑤正确,只要证明$\frac{AD}{AF}$=$\frac{\sqrt{2}}{2}$以及△ADG∽△AEF,利用相似三角形的面积比等于相似比的平方即可解决问题.
解答 解: ∵BA=BC,∠ABC=90°,AD=DC,
∵BA=BC,∠ABC=90°,AD=DC,
∴BD=DC=AD,∠C=∠CBD=∠ABD=∠CAB=45°,
∵△AEF是由△AEB翻折,
∴∠AFB=∠ABE=90°,∠EBG=∠EFG=45°,AF=AB,
∴∠AFG=∠C=45°,
∴FG∥BC,故②正确,
∵∠AFG=∠EFG=45°,
∴点E关于FG的对称点在直线FA上,故③错误,
∵∠C=45°,∠CFE=90°,
∴∠C=∠FEC=45°,
∴CF=EF,
设EB=EF=FC=a,则EC=$\sqrt{2}$a,AB=BC=($\sqrt{2}$+1)a,
∵∠EAB=∠EAF,
∴tan∠CAE=tan∠EAB=$\frac{EB}{AB}$=$\frac{1}{\sqrt{2}+1}$,故①错误.
∵AF=AB=($\sqrt{2}$+1)a,AB=($\sqrt{2}$+2)a,
∴AD=($\frac{\sqrt{2}}{2}$+1)a,
∴$\frac{AD}{AF}$=$\frac{\frac{\sqrt{2}}{2}+1}{\sqrt{2}+1}$=$\frac{\sqrt{2}}{2}$,
∵FG∥EB,BG∥EF,
∴四边形EFGB是平行四边形,
∵EB=EF,
∴四边形EFGB是菱形,
∴EB=GB,故④正确,
∵DG∥EF,
∴△ADG∽△AEF,
∴$\frac{{S}_{△ADG}}{{S}_{△AEF}}$=($\frac{AD}{AF}$)2=$\frac{1}{2}$,
∴S四边形DFEG=S△ADG故⑤正确.
故选C.
点评 本题考查翻折变换、等腰直角三角形的性质、相似三角形的性质等知识,利用翻折不变性是解决问题的关键,注意面积问题转化为相似三角形的面积比问题,属于中考常考题型.

| A. | 2×2-2=$\frac{1}{2}$ | B. | (-9)0=-1 | C. | 3a-2=$\frac{1}{3{a}^{2}}$(a≠0) | D. | a5×a-3=a5÷a3 |
| A. | $\sqrt{12}$与$\sqrt{24}$ | B. | $\sqrt{18}$与$\sqrt{24}$ | C. | $\sqrt{8}$与$\sqrt{18}$ | D. | $\sqrt{45}$与$\sqrt{12}$ |
 如图,已知直线AB∥CD,BC∥DE,若∠B=60°,则∠D=120°.
如图,已知直线AB∥CD,BC∥DE,若∠B=60°,则∠D=120°.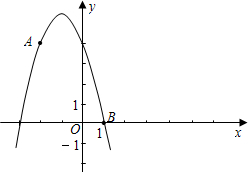 如图,已知A(-2,4)和B(1,0)都在抛物线$y=-\frac{4}{3}{x^2}-\frac{8}{3}x+4$
如图,已知A(-2,4)和B(1,0)都在抛物线$y=-\frac{4}{3}{x^2}-\frac{8}{3}x+4$