题目内容
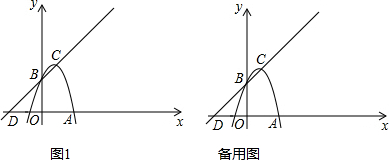
12. 如图,已知A(2$\sqrt{3}$,2)、B(2$\sqrt{3}$,1),将△AOB绕着点O逆时针旋转90°,到达△A′B′O的位置,则图中图形ABB′A′的周长为$\frac{\sqrt{13}}{2}$π+2π+2.
如图,已知A(2$\sqrt{3}$,2)、B(2$\sqrt{3}$,1),将△AOB绕着点O逆时针旋转90°,到达△A′B′O的位置,则图中图形ABB′A′的周长为$\frac{\sqrt{13}}{2}$π+2π+2.
分析 先利用点A,B的坐标求出OA,OB,AB,再求出两条弧长,计算即可.
解答 解:∵△AOB绕着点O逆时针旋转90°,到达△A′B′O的位置,
∴旋转角∠BOB′=∠AOA′=90°,
∵A(2$\sqrt{3}$,2)、B(2$\sqrt{3}$,1),
∴OA=4,OB=$\sqrt{13}$,AB=1,
由旋转得,A′B′=1,
∴$\widehat{AA′}$长═$\frac{90×π×4}{180}$=2π,
$\widehat{BB′}$长=$\frac{90×π×\sqrt{13}}{180}$=$\frac{\sqrt{13}}{2}$π,
∴图形ABB′A′的周长为$\frac{\sqrt{13}}{2}$π+2π+2.
故答案为$\frac{\sqrt{13}}{2}$π+2π+2
点评 此题是旋转的性质题,主要考查了旋转的性质,弧长公式,平面坐标系中距离公式,解本题的关键是弧长公式得熟记.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
7.已知x=$\sqrt{3}$+1,y=$\sqrt{3}$-1,则x2+2xy+y2的值为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
4.下面四个数中比-3小的数是( )
| A. | 2 | B. | 0 | C. | -2 | D. | -4 |
1.如图,AD、BE是△ABC的两条中线,则S△EDC:S△ABD等于( )
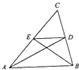

| A. | 1:2 | B. | 2:3 | C. | 1:3 | D. | 1:4 |
2.如图,AB∥CD,点E在BC上,且CD=CE,∠D=72°,则∠B的度数为( )


| A. | 36° | B. | 68° | C. | 22° | D. | 16° |
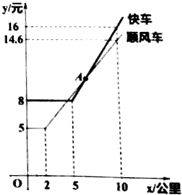 随着互联网的发展,互联网消费逐渐深入人们生活,如图是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象,下列说法:
随着互联网的发展,互联网消费逐渐深入人们生活,如图是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象,下列说法: