题目内容
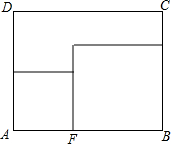如图，矩形纸片ABCD，AD=8，AB=10，点F在AB上，分别以AF、FB为边裁出的两个小正方形纸片面积和S的取值范围是考点：二次函数的应用
专题：
分析：设AF=x，则BF=10-x，由正方形的面积公式就可以得出S与x的关系，再由x的取值范围就可以确定S的取值范围．
解答：解：设AF=x，则BF=10-x，由题意，得
S=x2+（10-x）2，
S=2x2-20x+100，
S=2（x-5）2+50．
∴a=2＞0，
∴x=5时，S最小=50．
∵2≤x≤8，
当x=2时，S=68，
当x=8时，S=68．
∴50≤S≤68．
故答案为：50≤S≤68．
S=x2+（10-x）2，
S=2x2-20x+100，
S=2（x-5）2+50．
∴a=2＞0，
∴x=5时，S最小=50．
∵2≤x≤8，
当x=2时，S=68，
当x=8时，S=68．
∴50≤S≤68．
故答案为：50≤S≤68．
点评：本题考查了正方形的性质的运用，二次函数的解析式的运用，自变量的取值范围的运用，解答时求出函数的解析式是关键．
练习册系列答案
相关题目
如图，在正五边形ABCDE中，对角线AC，BD相交于点F．