题目内容
已知a>0,且不等式1<ax<2恰有三个正数解,则当不等式2<ax<3含有最多的整数解时,正数a的取值范围为 .
考点:一元一次不等式组的整数解
专题:
分析:不等式1<ax<2两边同时除以a得到a的范围,然后根据不等式有三个正整数解即可求得a的范围.
解答:解:不等式1<ax<2两边同时除以a得:
<x<
,
不等式有三个正整数解,则2<
-
<4,解得:
<a<
,
不等式2<ax<3的解集是:
<x<
,
则不等式2<ax<3含有最多的整数解时:
-
=
取得最大值,则a的范围是:2<a<4.
故答案是:2<a<4.
| 1 |
| a |
| 2 |
| a |
不等式有三个正整数解,则2<
| 2 |
| a |
| 1 |
| a |
| 1 |
| 4 |
| 1 |
| 2 |
不等式2<ax<3的解集是:
| 2 |
| a |
| 3 |
| a |
则不等式2<ax<3含有最多的整数解时:
| 3 |
| a |
| 2 |
| a |
| 1 |
| a |
故答案是:2<a<4.
点评:此题考查的是一元一次不等式的解法和一元一次方程的解,根据x的取值范围,得出x的整数解,然后代入方程即可解出a的值.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
节约能源,从我做起,为响应号召,小李决定将家里的4只白炽灯全部换成节能灯,商场有功率为4w和5w两种型号的节能灯若干可供选择,则买到的节能灯都为同一型号的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列函数:①y=-x;②y=2x;③y=-
;④y=
(x<0). y随x的增大而减小的函数有( )
| 1 |
| x |
| 2 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,在四边形ABCD中,AB=CD,AD=BC,对角线AC、BD交于点O,则图中共有全等三角形
如图,在四边形ABCD中,AB=CD,AD=BC,对角线AC、BD交于点O,则图中共有全等三角形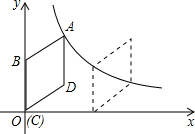 如图,直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在双曲线
如图,直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在双曲线