题目内容
3．若反比例函数y=$\frac{k}{x}$的图象经过点（1，2），那么y≥-2，x的取值范围是x≤-1或x＞0．分析 先求出k的值，再求出y=-2时x的值，根据反比例函数的性质即可得出结论．
解答 解：∵反比例函数y=$\frac{k}{x}$的图象经过点（1，2），
∴k=1×2=2＞0，
∴此函数图象的两个分支分别位于第一三象限．
∵当y=-2时，x=-1，
∴y≥-2时，x≤-1或x＞0．
故答案为：x≤-1或x＞0．
点评 本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
练习册系列答案
相关题目
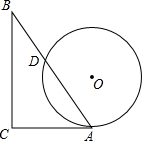如图，一个含有30°角的直角三角板ABC的直角边AC与⊙O相切于点A，∠C=90°，∠B=30°，⊙O的直径为4，AB与⊙O相交于D点，则AD的长为2$\sqrt{3}$．
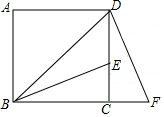如图，BD为正方形ABCD的对角线，BE平分∠DBC，交DC与点E，将△BCE绕点C按顺时针旋转90°得到△DCF，若CE=3cm，则FB=（6+3$\sqrt{2}$）cm．
如图，A，B是平面上的两定点，在平面上找一点C，使△ABC为等腰直角三角形，且点C为直角顶点，这样的点C有几个？
18．一项工程，甲单独做a小时完成，乙单独做b小时完成，甲、乙两人一起完成这项工程所需时间为（ ）
| A． | $\frac{ab}{a+b}$小时 | B． | $\frac{a+b}{ab}$小时 | C． | a+b小时 | D． | $\frac{1}{a+b}$小时 |
