题目内容
如图,点A、B为射线OM上两点,且OA=20cm,AB=60cm,点P以1cm/秒的速度从点O出发沿射线OM一直向右运动;同时点Q从点B出发向左运动.
(1)若点Q的速度为3cm/s,且运动到点O停止.
①经过 秒,P、Q两点相遇.
②经过多少秒,P、Q两点相距40cm.
(2)若点Q运动到点O后,仍以相同的速度返回到点B停止.当点P运动到PA=2PB,且点Q刚好运动到OB的中点时,求点Q运动的速度.

(1)若点Q的速度为3cm/s,且运动到点O停止.
①经过
②经过多少秒,P、Q两点相距40cm.
(2)若点Q运动到点O后,仍以相同的速度返回到点B停止.当点P运动到PA=2PB,且点Q刚好运动到OB的中点时,求点Q运动的速度.

考点:一元一次方程的应用,数轴,两点间的距离
专题:
分析:(1)①由相遇问题的数量关系直接由路程÷速度和=时间就可以求出结论;
②由相遇问题的数量关系,根据相遇前相距40厘米和相遇后相距40厘米分别求出其解即可;
(2)从题中我们可以看出点P及Q是运动的,不是静止的,当PA=2PB时实际上是P正好到了AB的三等分点上,而且PA=40,PB=20.由速度公式就可求出它的运动时间,即是点Q的运动时间,点Q运动到的位置恰好是线段AB的三等分点,这里的三等分点是二个点,因此此题就有二种情况,分别是OQ=
时,B是PA的中点时,由此就可建立方程求出它的速度.则设点Q运动的速度为xcm/秒,根据点P运动的时间=点Q运动的时间相等建立方程求出其解即可;
②由相遇问题的数量关系,根据相遇前相距40厘米和相遇后相距40厘米分别求出其解即可;
(2)从题中我们可以看出点P及Q是运动的,不是静止的,当PA=2PB时实际上是P正好到了AB的三等分点上,而且PA=40,PB=20.由速度公式就可求出它的运动时间,即是点Q的运动时间,点Q运动到的位置恰好是线段AB的三等分点,这里的三等分点是二个点,因此此题就有二种情况,分别是OQ=
| BO |
| 2 |
解答:解:(1)①∵点A、B为射线OM上两点,且OA=20cm,AB=60cm,点P以1cm/秒的速度从点O出发沿射线OM一直向右运动;
同时点Q从点B出发向左运动,点Q的速度为3cm/s,
∴
=20(秒).
故答案为:20;
②当两点相遇前相距40cm,则
=10(秒),
当两点相遇后相距40cm,点Q的速度为3cm/s,则
秒到达O点,
则P点运动40秒后就是两点之间的距离40cm,
故10秒或40秒,P、Q两点相距40cm;
(2)设点Q运动的速度为xcm/秒,由题意,得
=
,
解得:x=
.
当
=
,
解得:x=2,
当
=
,
解得:x=
,
当
=
,
解得:x=
.
经检验,x=
,
,
或2都是原方程的解.
答:点Q运动的速度
cm/秒,
cm/秒,
cm/秒,2cm/秒.
同时点Q从点B出发向左运动,点Q的速度为3cm/s,
∴
| 20+60 |
| 1+3 |
故答案为:20;
②当两点相遇前相距40cm,则
| 20+60-40 |
| 4 |
当两点相遇后相距40cm,点Q的速度为3cm/s,则
| 80 |
| 3 |
则P点运动40秒后就是两点之间的距离40cm,
故10秒或40秒,P、Q两点相距40cm;
(2)设点Q运动的速度为xcm/秒,由题意,得
| 60 |
| 1 |
| 40 |
| x |
解得:x=
| 2 |
| 3 |
当
| 60 |
| 1 |
| 120 |
| x |
解得:x=2,
当
| 140 |
| 1 |
| 40 |
| x |
解得:x=
| 2 |
| 7 |
当
| 140 |
| 1 |
| 120 |
| x |
解得:x=
| 6 |
| 7 |
经检验,x=
| 2 |
| 7 |
| 6 |
| 7 |
| 2 |
| 3 |
答:点Q运动的速度
| 2 |
| 7 |
| 6 |
| 7 |
| 2 |
| 3 |
点评:本题考查了数轴的运用,两点间的距离的运用,列一元一次方程解实际问题的运用,一元一次方程的解答的运用,解答时理清题目的数量关系建立方程是关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
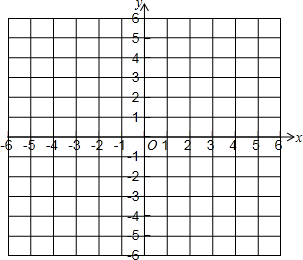 已知△ABC三个顶点的坐标分别是 A(-3,-1)、B(1,3)、C(2,-3)
已知△ABC三个顶点的坐标分别是 A(-3,-1)、B(1,3)、C(2,-3)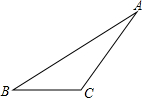 如图,在△ABC中,
如图,在△ABC中,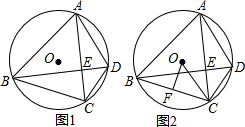 点A、B、C、D在⊙O上,AC⊥BD于点E,
点A、B、C、D在⊙O上,AC⊥BD于点E,
 如图为手的示意图,在各个手指间标记字母A、B、C、D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4…,当数到13时,对应的字母是
如图为手的示意图,在各个手指间标记字母A、B、C、D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始数连续的正整数1,2,3,4…,当数到13时,对应的字母是