题目内容
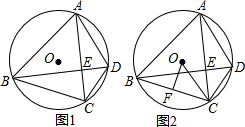 点A、B、C、D在⊙O上,AC⊥BD于点E,
点A、B、C、D在⊙O上,AC⊥BD于点E,(1)在图1中有几对相似三角形?请选一对加以证明.
(2)如图2,过O作OF⊥BC于点F,
①求证:△AEB∽△OFC,
②若OF=3,求AD的长.
考点:相似三角形的判定与性质,圆周角定理
专题:
分析:(1)利用圆周角定理以及相似三角形的判定得出即可;
(2)①利用圆周角定理得出∠BAC=∠FOC,进而得出△AEB∽△OFC;
②利用相似三角形的性质得出
=
,进而得出AD的长.
(2)①利用圆周角定理得出∠BAC=∠FOC,进而得出△AEB∽△OFC;
②利用相似三角形的性质得出
| OF |
| FC |
| AD |
| BC |
解答: 解:(1)△ABE∽△CDE,△ADE∽△BCE,有2对,
解:(1)△ABE∽△CDE,△ADE∽△BCE,有2对,
证明:∵∠BAC=∠BDC,∠AEB=∠CED,
∴△ABE∽△CDE,
∵∠EAD=∠CBE,∠AED=∠BCE,
∴△ADE∽△BCE;
(2)①证明:连接BO,
∵AC⊥BD,OF⊥BC,
∴∠AEB=90°,∠CFO=90°,
∵OF⊥BC,
∴∠COF=
∠BOC,
∵∠BAC=
∠BOC,
∴∠BAC=∠FOC,
∴△AEB∽△OFC;
②解:由①知,△AEB∽△OFC,
∴
=
,
∵△AED∽△BEC,
∴
=
,
∴
=
,
∵BC=2FC,
∴AD=2OF=6.
 解:(1)△ABE∽△CDE,△ADE∽△BCE,有2对,
解:(1)△ABE∽△CDE,△ADE∽△BCE,有2对,证明:∵∠BAC=∠BDC,∠AEB=∠CED,
∴△ABE∽△CDE,
∵∠EAD=∠CBE,∠AED=∠BCE,
∴△ADE∽△BCE;
(2)①证明:连接BO,
∵AC⊥BD,OF⊥BC,
∴∠AEB=90°,∠CFO=90°,
∵OF⊥BC,
∴∠COF=
| 1 |
| 2 |
∵∠BAC=
| 1 |
| 2 |
∴∠BAC=∠FOC,
∴△AEB∽△OFC;
②解:由①知,△AEB∽△OFC,
∴
| AE |
| BE |
| OF |
| FC |
∵△AED∽△BEC,
∴
| AE |
| BE |
| AD |
| BC |
∴
| OF |
| FC |
| AD |
| BC |
∵BC=2FC,
∴AD=2OF=6.
点评:此题主要考查了相似三角形的判定与性质和圆周角定理等知识,熟练利用圆周角定理得出相等的角是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
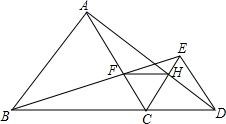 如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H,求证:FH∥BD.
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H,求证:FH∥BD.
 下面是小马虎解的一道题
下面是小马虎解的一道题