题目内容
7.已知二次函数y=mx2+6$\sqrt{3}$x+m+4的图象在直线y=-2的上方,求m的取值范围m>3.分析 根据题意,首先得出m>0,且顶点纵坐标大于-2,进而利用二次函数图象得出m的取值范围,进而得出答案.
解答  解:∵二次函数y=mx2+6$\sqrt{3}$x+m+4的图象在直线y=-2的上方,
解:∵二次函数y=mx2+6$\sqrt{3}$x+m+4的图象在直线y=-2的上方,
∴m>0,且顶点纵坐标大于-2,
则$\frac{4ac-{b}^{2}}{4a}$=$\frac{4m(m+4)-108}{4m}$>-2,
∴m2+6m-27>0,
当y=m2+6m-27=(m-3)(m+9),如图所示:
当y>0,则m<-9或m>3,
∵m>0,
∴m>3.
故答案为:m>3.
点评 此题主要考查了二次函数与不等式(组),利用数形结合得出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
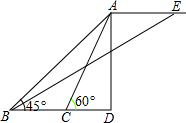 如图,广场上空有一个气球A,地面上点B、C、D在一条直线上,BC=20m,两个观测者在点B、C两处分别测得气球A的仰角∠ABD=45°,∠ACD=60°,当气球沿与BC的平行的路线飘移10秒后至达点E,在B处测得气球的仰角为30°.
如图,广场上空有一个气球A,地面上点B、C、D在一条直线上,BC=20m,两个观测者在点B、C两处分别测得气球A的仰角∠ABD=45°,∠ACD=60°,当气球沿与BC的平行的路线飘移10秒后至达点E,在B处测得气球的仰角为30°. 如图,若∠1=∠2,∠C=∠D.∠A和∠F是什么关系?为什么?
如图,若∠1=∠2,∠C=∠D.∠A和∠F是什么关系?为什么?