题目内容
 如图,已知∠1=50°,∠2=140°,CD⊥CE,则有DC∥AB,试说明理由.
如图,已知∠1=50°,∠2=140°,CD⊥CE,则有DC∥AB,试说明理由.考点:平行线的判定
专题:
分析:由条件结合垂直的定义可求得∠ACD=130°,由∠1可求得∠CAB,可得到∠CAB=∠ACD,可判定DC∥AB.
解答:解:DC∥AB,理由如下:
∵CD⊥CE,
∴∠DCE=90°,
又∠ACD+∠DCE+∠2=360°,
∴∠ACD=360°-90°-140°=130°,
又∠1+∠BAC=180°且∠1=50°,
∴∠BAC=130°,
∴∠BAC=∠ACD,
∴DC∥AB.
∵CD⊥CE,
∴∠DCE=90°,
又∠ACD+∠DCE+∠2=360°,
∴∠ACD=360°-90°-140°=130°,
又∠1+∠BAC=180°且∠1=50°,
∴∠BAC=130°,
∴∠BAC=∠ACD,
∴DC∥AB.
点评:本题主要考查平行线的判定,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c?a∥c.

练习册系列答案
相关题目
 如图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试画出一个三角形使边长为3
如图是由16个边长为1的小正方形拼成的,任意连结这些小正方形的若干个顶点,可得到一些线段,试画出一个三角形使边长为3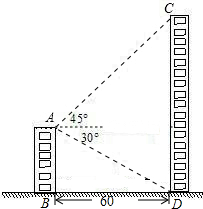 如图,小明在顶楼A处测得对面大楼楼顶点C处的仰角为45°,楼底点D处的俯角为30°,若两座楼AB与CD相距60米,求楼CD的高度约为多少米(结果保留三个有效数字).
如图,小明在顶楼A处测得对面大楼楼顶点C处的仰角为45°,楼底点D处的俯角为30°,若两座楼AB与CD相距60米,求楼CD的高度约为多少米(结果保留三个有效数字).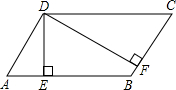 如图,已知?ABCD中,DE⊥AB于E,DF⊥BC于F,且∠EDF=60°,DE:DF=2:3,?ABCD的周长是50,求?ABCD各边的长.
如图,已知?ABCD中,DE⊥AB于E,DF⊥BC于F,且∠EDF=60°,DE:DF=2:3,?ABCD的周长是50,求?ABCD各边的长. 已知几何体主视图和俯视图如图所示
已知几何体主视图和俯视图如图所示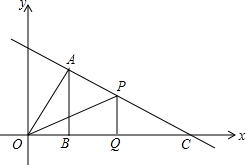 如图,一次函数y=-
如图,一次函数y=- 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点.求∠ECD的度数.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点.求∠ECD的度数. 如图,
如图,