题目内容
18.若直线l1:y=k1x+b1与l2:y=k2x+b2的交点在直线l上,则把直线l叫做l1、l2的“轨线”.(1)求l1:y=-x+3m-1与l2:y=x+m-1的“轨线”l的解析式;
(2)若l1:y=2x+b1与l2:y=-2x+b的交点在y=x+2上,且l1、l2的“轨线”为y=-x,求l1、l2的解析式.
分析 (1)由$\left\{\begin{array}{l}{y=-x+3m-1}\\{y=x+m-1}\end{array}\right.$,消去m可得y=2x-1,根据“轨线”的定义可知,l1:y=-x+3m-1与l2:y=x+m-1的“轨线”l的解析式为y=2x-1;
(2)由$\left\{\begin{array}{l}{y=x+2}\\{y=-x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$,由题意点(-1,1)在l1:y=2x+b1与l2:y=-2x+b2上,可得b1=3,b2=-1.
解答 (1)解:由$\left\{\begin{array}{l}{y=-x+3m-1}\\{y=x+m-1}\end{array}\right.$,消去m可得y=2x-1,
根据“轨线”的定义可知,l1:y=-x+3m-1与l2:y=x+m-1的“轨线”l的解析式为y=2x-1.
(2)解:由$\left\{\begin{array}{l}{y=x+2}\\{y=-x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$,
由题意点(-1,1)在l1:y=2x+b1与l2:y=-2x+b2上,
∴b1=3,b2=-1.
∴l1:y=2x+3,l2:y=-2x-1.
点评 本题考查了两条直线平行或相交的问题,一元一次方程组的应用、解题的关键是理解题意,学会用转化的思想思考问题,把问题转化为方程组解决,属于中考创新题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.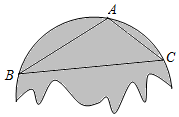 小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( )
小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( )
 小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( )
小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( )| A. | AB,AC边上的中线的交点 | B. | AB,AC边上的垂直平分线的交点 | ||
| C. | AB,AC边上的高所在直线的交点 | D. | ∠BAC与∠ABC的角平分线的交点 |
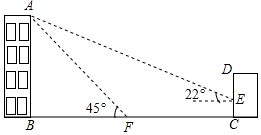 如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).
如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).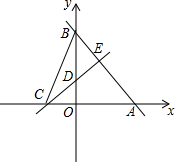 如图,直线y=-$\frac{4}{3}$x+8分别交x轴、y轴于A,B两点.线段AB的垂直平分线分别交x轴、y轴于C,D两点.
如图,直线y=-$\frac{4}{3}$x+8分别交x轴、y轴于A,B两点.线段AB的垂直平分线分别交x轴、y轴于C,D两点.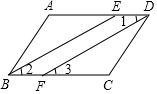 如图,在?ABCD中,BE,DF分别平分∠ABC,∠ADC.求证:BE∥DF.
如图,在?ABCD中,BE,DF分别平分∠ABC,∠ADC.求证:BE∥DF.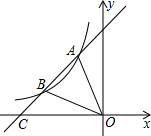 如图,直线y=mx+b与反比例函数y=$\frac{k}{x}$(x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
如图,直线y=mx+b与反比例函数y=$\frac{k}{x}$(x<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4. (1)如图,MN∥EF,GH∥EF,∠CAB=90°,∠1=70°,求:∠ABF的度数.
(1)如图,MN∥EF,GH∥EF,∠CAB=90°,∠1=70°,求:∠ABF的度数.