题目内容
 如图所示,直角三角尺放在一条直线上,求∠1+∠2的度数.
如图所示,直角三角尺放在一条直线上,求∠1+∠2的度数.考点:对顶角、邻补角,直角三角形的性质
专题:
分析:由对顶角相等得到∠1+∠2=∠3+∠4;然后根据直角三角形的两个锐角互余的性质进行解答.
解答: 解:如图,∵∠A=90°,
解:如图,∵∠A=90°,
∴∠3+∠4=90°.
∵∠1=∠3,∠2=∠4,
∴∠1+∠2=∠3+∠4=90°.即∠1+∠2=90°.
 解:如图,∵∠A=90°,
解:如图,∵∠A=90°,∴∠3+∠4=90°.
∵∠1=∠3,∠2=∠4,
∴∠1+∠2=∠3+∠4=90°.即∠1+∠2=90°.
点评:本题考查了对顶角、邻补角和直角三角形的性质.解题时利用了对顶角的性质:对顶角相等.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
下列4个命题:①矩形的对角线互相平分且相等;②对角线互相垂直的四边形是菱形;③等腰梯形的两条对角线相等;④等腰三角形底边上的中点到两腰的距离相等.其中正确的是( )
| A、①②③ | B、②③④ |
| C、①②④ | D、①③④ |
把方程4y+
=1+x写成用含x的代数式表示y的形式,以下各式正确的是( )
| x |
| 3 |
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|

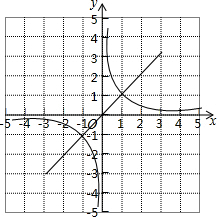 如图是函数y=x与y=
如图是函数y=x与y=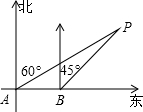 如图,海上有一灯塔P,在它周围15海里处有暗礁,一艘客轮以18海里/时的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶40分钟后,到达B处又测得灯塔P在它的北偏东45°方向,问客轮不改变方向继续前进有无触礁的危险?(参考数据
如图,海上有一灯塔P,在它周围15海里处有暗礁,一艘客轮以18海里/时的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶40分钟后,到达B处又测得灯塔P在它的北偏东45°方向,问客轮不改变方向继续前进有无触礁的危险?(参考数据 已知,如图,∠C=90°,∠A=30°,BD⊥AD于D,DC∥AB,AB=10,求CD的长.
已知,如图,∠C=90°,∠A=30°,BD⊥AD于D,DC∥AB,AB=10,求CD的长.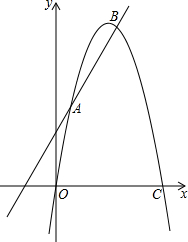 如图所示,已知抛物线y=ax2+bx+c与直线y=kx+4相交于A(1,5),B(4,8)两点,与x轴交于原点O及C点.
如图所示,已知抛物线y=ax2+bx+c与直线y=kx+4相交于A(1,5),B(4,8)两点,与x轴交于原点O及C点.