题目内容
如图，在梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，若AD=1，BC=3，则S△AOD：S△BOC的值为考点：相似三角形的判定与性质,梯形
专题：
分析：如图，证明△AOD∽△COB，列出比例式
=(
)2，求出
即可解决问题．
| S△AOD |
| S△BOC |
| AD |
| BC |
| AD |
| BC |
解答：解：如图，∵AD∥BC，
∴△AOD∽△COB，
∴
=(
)2，而AD=1，BC=3，
∴S△AOD：S△BOC的值为1：9，
故答案为1：9．
解：如图，∵AD∥BC，∴△AOD∽△COB，
∴
| S△AOD |
| S△BOC |
| AD |
| BC |
∴S△AOD：S△BOC的值为1：9，
故答案为1：9．
点评：该题主要考查了相似三角形的判定及其性质等几何知识点及其应用问题；应牢固掌握相似三角形的判定及其性质．
练习册系列答案
相关题目
如图，CE⊥AF，垂足为E，CE与BF相交于点D，∠F=40°，∠C=30°，求∠EDF、∠DBC的度数．
如图，AB是⊙O的直径，弦CD⊥AB于点N，点M在⊙O上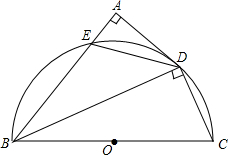
如图，BC为半圆的直径，O为圆心，BC=10，AD与半圆相切于点D，AB交⊙O于点E，DA⊥AB，AD=4 
已知，如图，在△ABC中，∠ACB=90°，CB=6，AB=12，求∠A，∠B的度数．
某市在“旧城改造”中，计划在市内一块如图所示的三角形空地中种植草皮美化环境，已知这种草皮每平方米要80元，求买这种草皮至少需多少元．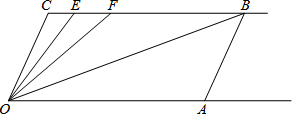
已知：如图，射线CB∥OA，∠C=∠OAB=120°，OE平分∠COF 交BC于点E，F在BC上，且满足OB平分∠AOF．