题目内容
 如图,CE⊥AF,垂足为E,CE与BF相交于点D,∠F=40°,∠C=30°,求∠EDF、∠DBC的度数.
如图,CE⊥AF,垂足为E,CE与BF相交于点D,∠F=40°,∠C=30°,求∠EDF、∠DBC的度数.考点:直角三角形的性质
专题:
分析:根据直角三角形两锐角互余列式计算即可求出∠EDF,再根据三角形的内角和定理求出∠C+∠DBC=∠F+∠DEF,然后求解即可.
解答:解:∵CE⊥AF,
∴∠DEF=90°,
∴∠EDF=90°-∠F=90°-40°=50°;
由三角形的内角和定理得,∠C+∠DBC=∠F+∠DEF,
所以,30°+∠DBC=40°+90°,
所以,∠DBC=100°.
∴∠DEF=90°,
∴∠EDF=90°-∠F=90°-40°=50°;
由三角形的内角和定理得,∠C+∠DBC=∠F+∠DEF,
所以,30°+∠DBC=40°+90°,
所以,∠DBC=100°.
点评:本题考查了直角三角形的性质,主要利用了直角三角形两锐角互余的性质,三角形的内角和定理,熟记性质并准确识图是解题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 如图,在矩形ABCD中,点F在CB的延长线上,AE=EF,CF=CA,求证:BE⊥DE.
如图,在矩形ABCD中,点F在CB的延长线上,AE=EF,CF=CA,求证:BE⊥DE. 已知AM是△ABC的中线.
已知AM是△ABC的中线.
 如图,在△ABC中,已知AB=AC,点D在AC上,AD=DB=BC,求∠A的度数.
如图,在△ABC中,已知AB=AC,点D在AC上,AD=DB=BC,求∠A的度数. 如图,在?ABCD的对角线BD上取两点E,G,使BE=DG,在对角线AC的延长线上取两点F,H,使AH=CF,求证:四边形EFGH是平行四边形.
如图,在?ABCD的对角线BD上取两点E,G,使BE=DG,在对角线AC的延长线上取两点F,H,使AH=CF,求证:四边形EFGH是平行四边形.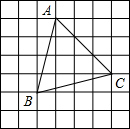 如图,方格纸中小正方形的边长为1,△ABC是格点三角形.
如图,方格纸中小正方形的边长为1,△ABC是格点三角形. 如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,若AD=1,BC=3,则S△AOD:S△BOC的值为
如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,若AD=1,BC=3,则S△AOD:S△BOC的值为