题目内容
在△ABC中,∠A=45°,AB=7,AC=4
,D、E、F分别是AB、BC、AC边上的动点.求△DEF的最小周长.
| 2 |
考点:轴对称-最短路线问题
专题:
分析:过B点作BM⊥AC于M,根据勾股定理求得AM=BM=
,进而求得CM=AC-AM=
,然后根据勾股定理求得BC=5,因为D、E、F分别是AB、BC、AC边上的中点时,E点关于AB的对称点E′,关于AC的对称点E″和D、F在一条直线上,△DEF有最小周长,根据三角形的中位线定理即可求得DE、EF、FD的值,进而求得△DEF的最小周长.
7
| ||
| 2 |
| ||
| 2 |
解答: 解:过B点作BM⊥AC于M,
解:过B点作BM⊥AC于M,
∵∠A=45°,
∴AM=BM=
,
∵AC=4
,
∴CM=AC-AM=
,
∴BC=
=5,
∵D、E、F分别是AB、BC、AC边上的中点时,E点关于AB的对称点E′,关于AC的对称点E″和D、F在一条直线上,△DEF有最小周长,
∴△DEF的最小周长=DE+EF+FD=
(AB+BC+CA)=
(7+5+4
)=6+2
.
 解:过B点作BM⊥AC于M,
解:过B点作BM⊥AC于M,∵∠A=45°,
∴AM=BM=
7
| ||
| 2 |
∵AC=4
| 2 |
∴CM=AC-AM=
| ||
| 2 |
∴BC=
| BM2+CM2 |
∵D、E、F分别是AB、BC、AC边上的中点时,E点关于AB的对称点E′,关于AC的对称点E″和D、F在一条直线上,△DEF有最小周长,
∴△DEF的最小周长=DE+EF+FD=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
点评:本题考查了勾股定理的应用,三角形的中位线定理,轴对称的性质和两点之间线段最短的性质等,应用勾股定理求得BC的长是本题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
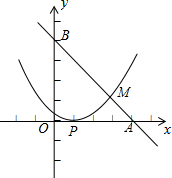 已知,如图,直线l经过A(4,0)和B(0,4)两点,抛物线y=a(x-h)2的顶点为P(1,0),直线l与抛物线的交点为M.
已知,如图,直线l经过A(4,0)和B(0,4)两点,抛物线y=a(x-h)2的顶点为P(1,0),直线l与抛物线的交点为M. 如图,已知△ABC在坐标平面内的顶点C(2,0),∠ACB=90°,∠B=30°,AB=6
如图,已知△ABC在坐标平面内的顶点C(2,0),∠ACB=90°,∠B=30°,AB=6 如图所示,∠A=∠C,求证:∠ADB=∠CEB.
如图所示,∠A=∠C,求证:∠ADB=∠CEB.