题目内容
1. 如图在△ABC中,M是BC的中点,S△ABC=16,则S△ABM是( )
如图在△ABC中,M是BC的中点,S△ABC=16,则S△ABM是( )| A. | 12 | B. | 8 | C. | 6 | D. | 4 |
分析 根据AM是△ABC的中线,于是得到结论.
解答 解:∵M是BC的中点,
∴AM是△ABC的中线,
∴S△ABM=$\frac{1}{2}$S△ABC=$\frac{1}{2}×$16=8,
故选B.
点评 本题考查了三角形的面积,熟记等底等高的三角形的三角形相等是解题的关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
12.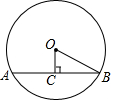 如图,在⊙O中,OC⊥AB于点C,AB=4,OC=1,则⊙O半径的长是( )
如图,在⊙O中,OC⊥AB于点C,AB=4,OC=1,则⊙O半径的长是( )
 如图,在⊙O中,OC⊥AB于点C,AB=4,OC=1,则⊙O半径的长是( )
如图,在⊙O中,OC⊥AB于点C,AB=4,OC=1,则⊙O半径的长是( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{15}$ | D. | $\sqrt{17}$ |
9.下列方程中是关于x的一元二次方程的是( )
| A. | 2x2-xy+5=0 | B. | (x-2)(x+1)=1 | C. | ax2+bx+c=0 | D. | x2+$\frac{1}{{x}^{2}}$=0 |
13.下列命题中,真命题是( )
| A. | 关于x的方程(m2+1)x2-3x+n=0不一定是一元二次方程 | |
| B. | 若点P是线段AB的黄金分割点,且AB=100,则AP≈61.8 | |
| C. | 等腰三角形的外心一定在它的内部 | |
| D. | 等弧所对的弦相等 |
10. 边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB′C′D′,两图叠成一个“蝶形风筝”(如图所示阴影部分),则这个风筝的面积是( )
边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB′C′D′,两图叠成一个“蝶形风筝”(如图所示阴影部分),则这个风筝的面积是( )
 边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB′C′D′,两图叠成一个“蝶形风筝”(如图所示阴影部分),则这个风筝的面积是( )
边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB′C′D′,两图叠成一个“蝶形风筝”(如图所示阴影部分),则这个风筝的面积是( )| A. | 2 | B. | $\frac{2\sqrt{3}}{3}$ | C. | 2-$\frac{\sqrt{3}}{4}$ | D. | 2-$\frac{\sqrt{3}}{3}$ |
11.若3y-6x=0,则x:y等于( )
| A. | 1:2 | B. | 2:1 | C. | -1:2 | D. | -2:1 |
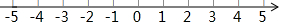 数轴如图所示,若点A,B在数轴上,点A与原点的距离为1个单位长度,点B与点A相距2个单位长度,则满足条件的所有点B与原点的距离的和是( )
数轴如图所示,若点A,B在数轴上,点A与原点的距离为1个单位长度,点B与点A相距2个单位长度,则满足条件的所有点B与原点的距离的和是( ) 如图所示,已知点O是直线AB上一点,OD平分∠AOC,OE平分∠BOC,且∠AOD=2∠COE,求∠BOE的度数.
如图所示,已知点O是直线AB上一点,OD平分∠AOC,OE平分∠BOC,且∠AOD=2∠COE,求∠BOE的度数.