题目内容
12.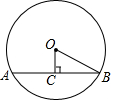 如图,在⊙O中,OC⊥AB于点C,AB=4,OC=1,则⊙O半径的长是( )
如图,在⊙O中,OC⊥AB于点C,AB=4,OC=1,则⊙O半径的长是( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{15}$ | D. | $\sqrt{17}$ |
分析 由垂径定理得出AC=$\frac{1}{2}$AB=2,再根据勾股定理可得答案.
解答 解:∵OC⊥AB于点C,
∴AC=$\frac{1}{2}$AB=2.
根据勾股定理,得
OB=$\sqrt{O{C}^{2}+B{C}^{2}}$=$\sqrt{5}$.
故选:B.
点评 此题综合运用了垂径定理和勾股定理;熟练掌握垂径定理是解决问题的关键.

练习册系列答案
相关题目
3.半径是R的圆的周长C=2πR,下列说法正确的是( )
| A. | C、π、R是变量 | B. | C是变量,2、π、R是常量 | ||
| C. | R是变量,2、π、C是常量 | D. | C、R是变量,2、π是常量 |
20.下列语句中不是命题的有( )
(1)两点之间,线段最短;
(2)连接A、B两点;
(3)鸟是动物;
(4)不相交的两条直线叫做平行线;
(5)无论a为怎样的有理数,式子a2+1的值都是正数吗?
(1)两点之间,线段最短;
(2)连接A、B两点;
(3)鸟是动物;
(4)不相交的两条直线叫做平行线;
(5)无论a为怎样的有理数,式子a2+1的值都是正数吗?
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.用代数式表示“a与b两数平方的差”,正确的是( )
| A. | (a-b)2 | B. | a-b2 | C. | a2-b2 | D. | a2-b |
17.在硬地上掷1枚图钉,通常会出现两种情况:“钉尖着地”与“钉尖不着地”.任意重复抛掷1枚图钉很多次时,你认为是哪种情况的可能性大( )
| A. | 钉尖着地 | B. | 钉尖不着地 | C. | 一样大 | D. | 不能确定 |
4.长为9,6,5,3的四根木条,选其中三根组成三角形,选法有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
1. 如图在△ABC中,M是BC的中点,S△ABC=16,则S△ABM是( )
如图在△ABC中,M是BC的中点,S△ABC=16,则S△ABM是( )
 如图在△ABC中,M是BC的中点,S△ABC=16,则S△ABM是( )
如图在△ABC中,M是BC的中点,S△ABC=16,则S△ABM是( )| A. | 12 | B. | 8 | C. | 6 | D. | 4 |
2.平面直角坐标系中,点M(-3,2)到y轴的距离是( )
| A. | 3 | B. | 2 | C. | 3或2 | D. | -3 |