题目内容
11. 如图,两个反比例函数y=$\frac{1}{x}$和y=$\frac{-2}{x}$的图象分别是C1和C2,点P是C1上自左向右运动的动点,PD⊥x轴,垂足为C,交C2于点D,PA⊥y轴,垂足为B,交C2于点A,则关于四边形ABCD的面积说法正确的是( )
如图,两个反比例函数y=$\frac{1}{x}$和y=$\frac{-2}{x}$的图象分别是C1和C2,点P是C1上自左向右运动的动点,PD⊥x轴,垂足为C,交C2于点D,PA⊥y轴,垂足为B,交C2于点A,则关于四边形ABCD的面积说法正确的是( )| A. | 逐渐变大 | B. | 逐渐变小 | C. | 不变,面积为$\frac{9}{2}$ | D. | 不变,面积为4 |
分析 设P的坐标是(a,$\frac{1}{a}$),推出点A和点D的坐标,求出∠APD=90°,求出PA、PD的值,根据三角形的面积公式求出△PAD的面积;根据反比例函数系数k的几何意义,得出△PBC的面积=$\frac{1}{2}$矩形OBPC的面积=$\frac{1}{2}$;然后根据四边形ABCD的面积=△PAD的面积-△PBC的面积计算即可.
解答 解:∵点P在y=$\frac{1}{x}$的图象上,
∴|xp|×|yp|=|k|=1,
∴设P的坐标是(a,$\frac{1}{a}$)(a为正数),
∵PD⊥x轴,
∴D的横坐标是a,
∵D在y=$\frac{-2}{x}$的图象上,
∴D的坐标是(a,-$\frac{2}{a}$),
∵PA⊥y轴,
∴A的纵坐标是$\frac{1}{a}$,
∵A在y=$\frac{-2}{x}$的图象上,
∴代入得:$\frac{1}{a}$=-$\frac{2}{x}$, 解得:x=-2a,
解得:x=-2a,
∴A的坐标是(-2a,$\frac{1}{a}$),
∴PA=a-(-2a)=3a,PD=$\frac{1}{a}$-(-$\frac{2}{a}$)=$\frac{3}{a}$,
∵PA⊥y轴于B,PD⊥y轴于C,x轴⊥y轴,
∴PA⊥PD,四边形OBPC是矩形,
∴△PAD的面积是:$\frac{1}{2}$PA×PD=$\frac{1}{2}$×3a×$\frac{3}{a}$=$\frac{9}{2}$;
∵点P在y=$\frac{1}{x}$的图象上,PA⊥y轴于B,PD⊥y轴于C,
∴△PBC的面积=$\frac{1}{2}$矩形OBPC的面积=$\frac{1}{2}$,
∴四边形ABCD的面积=△PAD的面积-△PBC的面积
=$\frac{9}{2}$-$\frac{1}{2}$=4.
故选D.
点评 此题主要考查了反比例函数系数k的几何意义和三角形面积公式的应用,根据已知得出△PAD面积与△PBC的面积是解决问题的关键.本题具有一定的代表性,是一道比较好的题目.

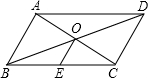 已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )| A. | OE=$\frac{1}{2}$DC | B. | OA=OC | C. | ∠BOE=∠OBA | D. | ∠OBE=∠OCE |
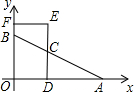 如图,在平面直角坐标系中,点A、B的坐标分别为(4,0)、(0,2),点C为线段AB上任意一点(不与点A、B重合),CD⊥OA于点D,点E在DC的延长线上,EF⊥y轴于点F,若点C为DE的中点,则四边形ODEF的周长为( )
如图,在平面直角坐标系中,点A、B的坐标分别为(4,0)、(0,2),点C为线段AB上任意一点(不与点A、B重合),CD⊥OA于点D,点E在DC的延长线上,EF⊥y轴于点F,若点C为DE的中点,则四边形ODEF的周长为( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
| A. | a | B. | |a| | C. | $\frac{1}{a}$ | D. | -a |
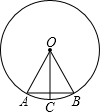 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )
如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )| A. | △OAB是等边三角形 | |
| B. | 弦AC的长等于圆内接正十二边形的边长 | |
| C. | OC平分弦AB | |
| D. | ∠BAC=30° |
 如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB等于( )
如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB等于( )| A. | 70° | B. | 20° | C. | 140° | D. | 35° |
 如图,点D为BA延长线上的一点,且∠B=45°,∠D=∠ACB=60°,AB=3$\sqrt{2}$,
如图,点D为BA延长线上的一点,且∠B=45°,∠D=∠ACB=60°,AB=3$\sqrt{2}$, 如图,小明在窗台C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知窗台C处离地面的距离CD为5m,则大树的高度为5+5$\sqrt{3}$m.(结果保留根号)
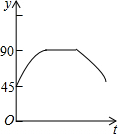
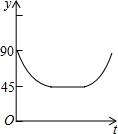
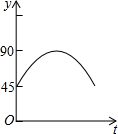
如图,小明在窗台C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知窗台C处离地面的距离CD为5m,则大树的高度为5+5$\sqrt{3}$m.(结果保留根号)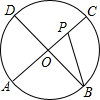 如图,AC、BD为圆O的两条互相垂直的直径,动点P从圆心O出发,沿O→C→D→O的路线在半径OC,劣弧$\widehat{CD}$,半径DO上作匀速运动,设运动时间为t秒,∠APB的度数为y度,那么表示y与t之间函数关系的图象大致为( )
如图,AC、BD为圆O的两条互相垂直的直径,动点P从圆心O出发,沿O→C→D→O的路线在半径OC,劣弧$\widehat{CD}$,半径DO上作匀速运动,设运动时间为t秒,∠APB的度数为y度,那么表示y与t之间函数关系的图象大致为( )