题目内容
6. 如图,点D为BA延长线上的一点,且∠B=45°,∠D=∠ACB=60°,AB=3$\sqrt{2}$,
如图,点D为BA延长线上的一点,且∠B=45°,∠D=∠ACB=60°,AB=3$\sqrt{2}$,(1)试求BC的长;
(2)尺规作图:作出△ADC的外接圆⊙O(不写作法,保留作图痕迹),并求出⊙O的半径.
分析 (1)作辅助线构建两个直角三角形,一个是45°的等腰直角三角形,一个是60°的直角三角形,分别求出BE和EC,并相加.
(2)分别作边DC和AC的垂直平分线,交点就是外接圆的圆心O;先求圆心角∠AOC=120°,在直角△OFC中利用勾股定理或三角函数求半径的长.
解答  解:(1)如图1,过A作AE⊥BC,垂足为E,
解:(1)如图1,过A作AE⊥BC,垂足为E,
在直角△ABE中,∵∠B=45°,
∴AE=BE,
由勾股定理得:AE2+BE2=AB2,
2AE2=(3$\sqrt{2}$)2,
AE2=9,
AE=±3,
∵AE>0,
∴AE=BE=3,
在直角△AEC中,∠ACB=60°,
∴tan60°=$\frac{AE}{EC}$,
∴EC=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$,
∴BC=BE+EC=3+$\sqrt{3}$.
(2)如图2,连接OA、OC,
∵∠D=60°,
∴∠AOC=120°,
∵OF是AC的垂直平分线,
∴∠FOC=$\frac{1}{2}$∠AOC=60°,
由勾股定理得:AC=$\sqrt{{3}^{2}+(\sqrt{3})^{2}}$=2$\sqrt{3}$,
∴FC=$\sqrt{3}$,
∴sin60°=$\frac{FC}{OC}$,
∴OC=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2,
∴⊙O的半径为2.
点评 本题考查了三角形的外接圆、等腰直角三角形的性质和三角函数等知识的综合应用.本题的关键是恰当的构建直角三角形,利用勾股定理或三角函数求边长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下列数中,-3的倒数是( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -3 | D. | 3 |
1.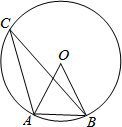 如图,△ABC是⊙O内接三角形,∠ACB=26°,则∠ABO的度数是( )
如图,△ABC是⊙O内接三角形,∠ACB=26°,则∠ABO的度数是( )
 如图,△ABC是⊙O内接三角形,∠ACB=26°,则∠ABO的度数是( )
如图,△ABC是⊙O内接三角形,∠ACB=26°,则∠ABO的度数是( )| A. | 64° | B. | 52° | C. | 54° | D. | 70° |
11. 如图,两个反比例函数y=$\frac{1}{x}$和y=$\frac{-2}{x}$的图象分别是C1和C2,点P是C1上自左向右运动的动点,PD⊥x轴,垂足为C,交C2于点D,PA⊥y轴,垂足为B,交C2于点A,则关于四边形ABCD的面积说法正确的是( )
如图,两个反比例函数y=$\frac{1}{x}$和y=$\frac{-2}{x}$的图象分别是C1和C2,点P是C1上自左向右运动的动点,PD⊥x轴,垂足为C,交C2于点D,PA⊥y轴,垂足为B,交C2于点A,则关于四边形ABCD的面积说法正确的是( )
 如图,两个反比例函数y=$\frac{1}{x}$和y=$\frac{-2}{x}$的图象分别是C1和C2,点P是C1上自左向右运动的动点,PD⊥x轴,垂足为C,交C2于点D,PA⊥y轴,垂足为B,交C2于点A,则关于四边形ABCD的面积说法正确的是( )
如图,两个反比例函数y=$\frac{1}{x}$和y=$\frac{-2}{x}$的图象分别是C1和C2,点P是C1上自左向右运动的动点,PD⊥x轴,垂足为C,交C2于点D,PA⊥y轴,垂足为B,交C2于点A,则关于四边形ABCD的面积说法正确的是( )| A. | 逐渐变大 | B. | 逐渐变小 | C. | 不变,面积为$\frac{9}{2}$ | D. | 不变,面积为4 |
18.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
15.下列实数中$\sqrt{7}$,-(-π),|-3|,3中,最大的是( )
| A. | $\sqrt{7}$ | B. | -(-π) | C. | |-3| | D. | 3 |
16.用一枚直径为25mm的硬币完全覆盖一个正六边形,则这个正六边形的最大边长是( )
| A. | $\frac{25}{2}$mm | B. | $\frac{25}{2}$$\sqrt{3}$mm | C. | $\frac{25}{4}$mm | D. | $\frac{25}{4}$$\sqrt{3}$mm |
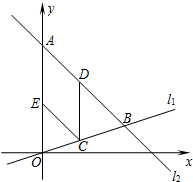 如图,在平面直角坐标系内,点A的坐标为(0,24 ),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
如图,在平面直角坐标系内,点A的坐标为(0,24 ),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).