题目内容
20.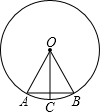 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )
如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )| A. | △OAB是等边三角形 | |
| B. | 弦AC的长等于圆内接正十二边形的边长 | |
| C. | OC平分弦AB | |
| D. | ∠BAC=30° |
分析 由OA=AB得出△0AB为等边三角形,再根据OC⊥AB可得出OC平分弧AB,得出弧AC等于弧BC,根据圆周角定理得出∠AOC=∠BOC=30°,再进行选择即可.
解答 解:∵OA=AB=OB,
∴△OAB是等边三角形,选项A正确,
∴∠AOB=60°,
∵OC⊥AB,
∴∠AOC=∠BOC=30°,AC=BC,弧AC=弧BC,
∴$\frac{360°}{30°}$=12,∠BAC=$\frac{1}{2}$∠BOC=15°,
∴选项B、C正确,选项D错误,
故选D.
点评 本题考查了正多边形的性质、垂径定理、圆周角定理以及等边三角形的判定和性质,要熟练应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.计算(ab2)3的结果,正确的是( )
| A. | a3b6 | B. | a3b5 | C. | ab6 | D. | ab5 |
11. 如图,两个反比例函数y=$\frac{1}{x}$和y=$\frac{-2}{x}$的图象分别是C1和C2,点P是C1上自左向右运动的动点,PD⊥x轴,垂足为C,交C2于点D,PA⊥y轴,垂足为B,交C2于点A,则关于四边形ABCD的面积说法正确的是( )
如图,两个反比例函数y=$\frac{1}{x}$和y=$\frac{-2}{x}$的图象分别是C1和C2,点P是C1上自左向右运动的动点,PD⊥x轴,垂足为C,交C2于点D,PA⊥y轴,垂足为B,交C2于点A,则关于四边形ABCD的面积说法正确的是( )
 如图,两个反比例函数y=$\frac{1}{x}$和y=$\frac{-2}{x}$的图象分别是C1和C2,点P是C1上自左向右运动的动点,PD⊥x轴,垂足为C,交C2于点D,PA⊥y轴,垂足为B,交C2于点A,则关于四边形ABCD的面积说法正确的是( )
如图,两个反比例函数y=$\frac{1}{x}$和y=$\frac{-2}{x}$的图象分别是C1和C2,点P是C1上自左向右运动的动点,PD⊥x轴,垂足为C,交C2于点D,PA⊥y轴,垂足为B,交C2于点A,则关于四边形ABCD的面积说法正确的是( )| A. | 逐渐变大 | B. | 逐渐变小 | C. | 不变,面积为$\frac{9}{2}$ | D. | 不变,面积为4 |
8. 如图,圆锥的母线长为5cm,高线长为4cm,则圆锥的底面积是( )
如图,圆锥的母线长为5cm,高线长为4cm,则圆锥的底面积是( )
 如图,圆锥的母线长为5cm,高线长为4cm,则圆锥的底面积是( )
如图,圆锥的母线长为5cm,高线长为4cm,则圆锥的底面积是( )| A. | 3πcm2 | B. | 9πcm2 | C. | 16πcm2 | D. | 25πcm2 |
15.下列实数中$\sqrt{7}$,-(-π),|-3|,3中,最大的是( )
| A. | $\sqrt{7}$ | B. | -(-π) | C. | |-3| | D. | 3 |
12. 已知:如图,在菱形ABCD中,∠BAD=44°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
已知:如图,在菱形ABCD中,∠BAD=44°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
 已知:如图,在菱形ABCD中,∠BAD=44°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
已知:如图,在菱形ABCD中,∠BAD=44°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )| A. | 112° | B. | 114° | C. | 116° | D. | 118° |
10.不等式x+7<3x+1的解集是( )
| A. | x<-3 | B. | x>3 | C. | x<-4 | D. | x>4 |
 定义:长宽比为$\sqrt{n}$:1(n为正整数)的矩形称为$\sqrt{n}$矩形,下面,我们通过折叠的方式折出一个$\sqrt{2}$矩形,如图①所示.
定义:长宽比为$\sqrt{n}$:1(n为正整数)的矩形称为$\sqrt{n}$矩形,下面,我们通过折叠的方式折出一个$\sqrt{2}$矩形,如图①所示. 如图,已知抛物线m:y=ax2-6ax+c(a>0)的顶点A在x轴上,并过点B(0,1),直线n:y=-$\frac{1}{2}$x+$\frac{7}{2}$与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(-7,7).
如图,已知抛物线m:y=ax2-6ax+c(a>0)的顶点A在x轴上,并过点B(0,1),直线n:y=-$\frac{1}{2}$x+$\frac{7}{2}$与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(-7,7).