题目内容
14.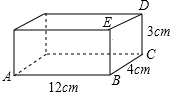 如图是一个长、宽、高分别为12cm,4cm,3cm的木箱,在它里面放入一根细木条(木条的粗细忽略不计),要求木条不能露出木箱,请你算一算,能放入的细木条的最大长度是多少?
如图是一个长、宽、高分别为12cm,4cm,3cm的木箱,在它里面放入一根细木条(木条的粗细忽略不计),要求木条不能露出木箱,请你算一算,能放入的细木条的最大长度是多少?
分析 直接利用勾股定理得出AC的长,进而得出AD的长.
解答  解:连接AC,AD,
解:连接AC,AD,
在Rt△ABC中,
AC2=AB2+BC2,
则AC=$\sqrt{1{2}^{2}+{4}^{2}}$=$\sqrt{160}$=4$\sqrt{10}$,
在Rt△ACD中,
AD2=AC2+DC2,
则AD=$\sqrt{160+9}$=13,
答:能放入的细木条的最大长度是13cm.
点评 此题主要考查了勾股定理,正确应用勾股定理是解题关键.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
2.已知12与a的积为-48,则a比4小( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
19. 从不同方向观察如图所示的几何体,不可能看到的是( )
从不同方向观察如图所示的几何体,不可能看到的是( )
 从不同方向观察如图所示的几何体,不可能看到的是( )
从不同方向观察如图所示的几何体,不可能看到的是( )| A. |  | B. |  | C. |  | D. |  |
 =____.
=____.



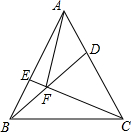 如图,已知在等边△ABC中,AB=AC=BC=8,点D、E分别是边AC、AB上两点,且AE=CD,BD交CE于F,连接AF,则AF的最小值为$\frac{8\sqrt{3}}{3}$.
如图,已知在等边△ABC中,AB=AC=BC=8,点D、E分别是边AC、AB上两点,且AE=CD,BD交CE于F,连接AF,则AF的最小值为$\frac{8\sqrt{3}}{3}$.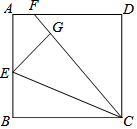 如图,已知正方形ABCD,E是AB的中点,F是AD上的一点,EG⊥CF于G且AF=$\frac{1}{4}$AD.
如图,已知正方形ABCD,E是AB的中点,F是AD上的一点,EG⊥CF于G且AF=$\frac{1}{4}$AD.