��Ŀ����
12����1���ⷽ����$\left\{{\begin{array}{l}{x-2y=4\;\;\;\;\;\;\;��1��\;\;\;\;}\\{2x+y-3=0\;\;\;��2��\;\;\;\;\;\;}\end{array}}$��2���ⲻ��ʽ��$\left\{\begin{array}{l}3��x-1����5x+1\\ \frac{x-1}{2}��2x-4\end{array}$����ָ���������еķǸ������⣮
��3���Ȼ�������ֵ��$\frac{{{b^2}-{a^2}}}{{{a^2}-ab}}�£�{a+\frac{{2ab+{b^2}}}{a}}��•��{\frac{1}{a}+\frac{1}{b}}��$������$a={��{\frac{1}{2}}��^{-1}}$+2sin60�㣬b=2��2014-�У�0-|-$\sqrt{3}$|��
���� ��1�����ô�����Ԫ���ⷽ���飻
��2���ȷֱ����������ʽ�õ�x��-2��$x��\frac{7}{3}$��Ȼ����ݡ���СС���м��ҡ�ȷ������ʽ��Ľ⼯�������������ʾ�⼯��
��3���Ȱ�������ͨ�֣��ٰѷ��ӷ�ĸ��ʽ�ֽ�ͳ������㻯Ϊ�˷����㣬����Լ�ֵõ�ԭʽ=-$\frac{1}{ab}$��Ȼ�������ָ���ݺ�����ָ���ݼ����a��b��ֵ���ٰ�a��b��ֵ����ԭʽ=-$\frac{1}{ab}$������ƽ���ʽ���㼴�ɣ�
��� �⣺��1��$\left\{{\begin{array}{l}{x-2y=4\;\;\;\;\;\;\;��1��\;\;\;\;}\\{2x+y-3=0\;\;\;��2��\;\;\;\;\;\;}\end{array}}$��
�ɣ�1���ã�x=4+2y�ۣ�
�ѣ�3�����루2���ã�2��4+2y��+y-3=0��
���y=-1��
��y=-1���루3����x=2��
���Է�����Ľ�Ϊ$\left\{{\begin{array}{l}{x=2}\\{y=-1}\end{array}}\right.$��
��2��$\left\{\begin{array}{l}3��{x-1}����5x+1��\;��\\ \frac{x-1}{2}��2x-4.\;\;\;��\end{array}\right.$
�ɢٵ�x��-2��
�ɢڵ�$x��\frac{7}{3}$��
��ԭ����ʽ��Ľ⼯��$-2��x��\frac{7}{3}$��
�����ķǸ�������Ϊ0��1��2��
��3��ԭʽ=-$\frac{��a-b����a+b��}{a��a-b��}$��$\frac{{a}^{2}+2ab+{b}^{2}}{a}$•$\frac{a+b}{ab}$
=-$\frac{��a+b����a-b��}{a��a-b��}$•$\frac{a}{��a+b��^{2}}$•$\frac{a+b}{ab}$
=-$\frac{1}{ab}$��
��a=2+2��$\frac{\sqrt{3}}{2}$=2+$\sqrt{3}$��b=2��1-$\sqrt{3}$=2-$\sqrt{3}$��
��ԭʽ=-$\frac{1}{��2+\sqrt{3}����2-\sqrt{3}��}$=-$\frac{1}{4-3}$=-1��
���� ���⿼���˷�ʽ�Ļ�����ֵ���Ȱѷ�ʽ������ٰѷ�ʽ��δ֪����Ӧ��ֵ���������ʽ��ֵ���ڻ���Ĺ�����Ҫע������˳��ͷ�ʽ�Ļ��������������ӡ���ĸҪ����Լ�֣�ע������Ľ��Ҫ��������ʽ����ʽ��Ҳ�����˽��Ԫһ�η������ʵ�������㣮

| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
| A�� | ����ʽx��ϵ���ʹ�������1 | |
| B�� | $\frac{1}{2}$���ǵ���ʽ | |
| C�� | ����ʽ3x2y+2xy-3x+y��һ�����ϵ���ֱ���-3��1 | |
| D�� | -$\frac{2xy}{3}$��ϵ��Ϊ-$\frac{2}{3}$�Ķ��ε���ʽ |
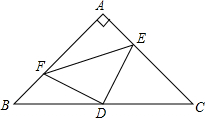 ��֪����ͼ��Rt��ABC�У���BAC=90�㣬AB=AC��D��BC���е㣬AE=BF��
��֪����ͼ��Rt��ABC�У���BAC=90�㣬AB=AC��D��BC���е㣬AE=BF�� ��ͼ����֪��EFD=��BCA��BC=EF��AF=DC����AB=DE����ͨ�����������յ���ʽ˵�����ɣ�
��ͼ����֪��EFD=��BCA��BC=EF��AF=DC����AB=DE����ͨ�����������յ���ʽ˵�����ɣ�