题目内容
18.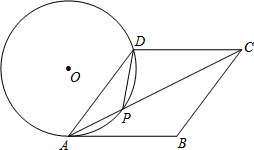 如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.
如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.(1)求证:AB为⊙O的切线;
(2)若⊙O的半径为$\frac{5\sqrt{5}}{4}$,tan∠DAC=$\frac{1}{2}$,求AC的长.
分析 (1)连结OP、OA,OP交AD于E,由PA=PD得弧AP=弧DP,根据垂径定理的推理得OP⊥AD,AE=DE,则∠1+∠OPA=90°,而∠OAP=∠OPA,所以∠1+∠OAP=90°,再根据菱形的性质得∠1=∠2,所以∠2+∠OAP=90°,然后根据切线的判定定理得到直线AB与⊙O相切;
(2)连接OP,OA,过点D作DE⊥AC于点E,由tan∠DAC=$\frac{1}{2}$可知DF=$\frac{1}{2}$AF,设AC=4a,则AF=2a,DF=a,AD=$\sqrt{5}$a,AE=$\frac{\sqrt{5}}{2}$a,OE=OP-PE=$\frac{5\sqrt{5}}{4}$-$\frac{\sqrt{5}}{4}$a,再根据勾股定理求出a的值,进而可得出AC的长.
解答 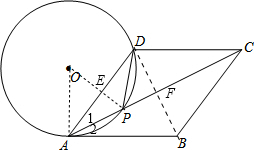 解:(1)直线AB与⊙O相切.理由如下:
解:(1)直线AB与⊙O相切.理由如下:
连结OP、OA,OP交AD于E,如图,
∵PA=PD,
∴弧AP=弧DP,
∴OP⊥AD,AE=DE,
∴∠1+∠OPA=90°,
∵OP=OA,
∴∠OAP=∠OPA,
∴∠1+∠OAP=90°,
∵四边形ABCD为菱形,
∴∠1=∠2,
∴∠2+∠OAP=90°,
∴OA⊥AB,
∴直线AB与⊙O相切;
(2)连结BD交AC于点F,则AC⊥BD.设⊙O的半径为r.
设AC=4a,
∴AF=2a,
∵tan∠DAC=$\frac{1}{2}$,
∴DF=a,
∴AD=$\sqrt{A{F}^{2}+D{F}^{2}}$=$\sqrt{5}$a,
∴AE=$\frac{1}{2}$AD=$\frac{\sqrt{5}}{2}$a,
在Rt△AEP中,∵tan∠DAC=$\frac{1}{2}$,
∴EP=$\frac{1}{2}$AE=$\frac{\sqrt{5}}{4}$a,
在Rt△AEO中,由勾股定理得:AE2+OE2=OA2,
即($\frac{\sqrt{5}}{2}$a)2+($\frac{5\sqrt{5}}{4}$-$\frac{\sqrt{5}}{4}$a)2=($\frac{5\sqrt{5}}{4}$)2,
解得:a=2,
∴AC=4a=8.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了菱形的性质和锐角三角函数以及勾股定理.

| A. | (x3)2=x5 | B. | x2•x3=x6 | C. | x3÷x=x2 | D. | (x2y)2=x4y |
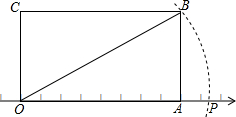 如图,矩形OABC的顶点O是数轴的原点,长边OA在数轴上,点A所表示的数为8,OC的长为$\sqrt{24}$,以O为圆心OB为半径的圆弧与数轴交于P点,则P点表示的数是( )
如图,矩形OABC的顶点O是数轴的原点,长边OA在数轴上,点A所表示的数为8,OC的长为$\sqrt{24}$,以O为圆心OB为半径的圆弧与数轴交于P点,则P点表示的数是( )| A. | 2$\sqrt{6}$ | B. | 9.5 | C. | 2$\sqrt{22}$ | D. | 4$\sqrt{11}$ |
| A. | x=$\frac{5}{2}$ | B. | 3 | C. | x1=-$\frac{5}{2}$,x2=-3 | D. | x1=3,x2=$\frac{5}{2}$ |
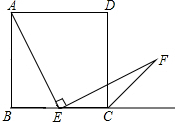 探索与证明:
探索与证明: 如图,在△ABC,∠B=50°,AE是∠BAC的平分线,∠ACD=120°,求∠AEC的度数.
如图,在△ABC,∠B=50°,AE是∠BAC的平分线,∠ACD=120°,求∠AEC的度数.
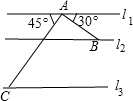 如图,三条平行的高速公路l1、l2、l3分别经过A、B、C三个城市,AB、AC分别为两条连接城市的普通公路,AB、AC分别与l1成30°、45°角,已知AB=200千米,AC=400千米,求两条高速公路l2、l3之间的距离(结果保留根号).
如图,三条平行的高速公路l1、l2、l3分别经过A、B、C三个城市,AB、AC分别为两条连接城市的普通公路,AB、AC分别与l1成30°、45°角,已知AB=200千米,AC=400千米,求两条高速公路l2、l3之间的距离(结果保留根号).