题目内容
13. 探索与证明:
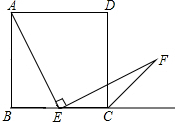
探索与证明:如图,四边形ABCD是正方形,点E是BC上的中点,EF⊥AE于点E,且EF交正方形外角的平分线CF于点F.
(1)求证:AE=EF;
(2)如果点E是BC边上异于B、C的任意一点,其他条件不变,AE=EF吗?并证明.
分析 (1)取AB的中点H,连接EH,根据已知及正方形的性质利用ASA判定△AHE≌△ECF,得出对应边相等即可;
(2)在AB上截取BH=BE,连接HE,则△BHE是等腰直角三角形,AH=CE,证出∠AHE=∠ECF,∠1=∠2,由ASA证明△AHE≌△ECF,得出对应边相等即可.
解答 (1)证明:取AB的中点H,连接EH;如图1所示:
则AH=BH=$\frac{1}{2}$AB,
∵四边形ABCD是正方形,
∴∠B=∠BCD=90°,AB=BC,
∵点E是BC上的中点,
∴BE=CE=$\frac{1}{2}$BC,
∴AH=BH=BE=CE,
∴△BEH是等腰直角三角形,
∴∠BHE=∠BEH=45°,
∴∠AHE=135°,
∵CF是正方形外角的平分线,
∴∠DCF=45°,
∴∠ECF=90°+45°=135°,
∴∠AHE=∠ECF,
∵AE⊥EF,
∴∠2+∠AEB=90°,
∵∠1+∠AEB=90°,
∴∠1=∠2,
在△AHE和△ECF中,$\left\{\begin{array}{l}{∠1=∠2}&{\;}\\{AH=CE}&{\;}\\{∠AHE=∠ECF}&{\;}\end{array}\right.$,
∴△AHE≌△ECF(ASA),
∴AE=EF;
(2)解:AE=EF;理由如下:
在AB上截取BH=BE,连接HE,如图2所示:
则△BHE是等腰直角三角形,AH=CE,
∴BHE=∠BEH=45°,
∴∠AHE=135°,
∴∠1+∠HEA=45°,
由(1)得:∠ECF=135°,
∴∠AHE=∠ECF,
∵AE⊥EF,
∴∠AEF=90°,
∴∠1+∠CEF=45°,
∴∠1=∠2,
在△AHE和△ECF中,$\left\{\begin{array}{l}{∠1=∠2}&{\;}\\{AH=CE}&{\;}\\{∠AHE=∠ECF}&{\;}\end{array}\right.$,
∴△AHE≌△ECF(ASA),
∴AE=EF.
点评 本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

 如图所示的“U”形几何体的主视图是( )
如图所示的“U”形几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
 图1是由6个小正方形组成的立体图形,它的左视图是( )
图1是由6个小正方形组成的立体图形,它的左视图是( )| A. |  | B. |  | C. |  | D. |  |
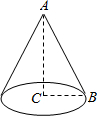 如图,△ABC中,∠ACB=90°,AC=4,BC=3,把△ABC绕AC边旋转一周(360°)得到一个圆锥体,那么这个圆锥体的侧面积为15π(结果可保留π)
如图,△ABC中,∠ACB=90°,AC=4,BC=3,把△ABC绕AC边旋转一周(360°)得到一个圆锥体,那么这个圆锥体的侧面积为15π(结果可保留π)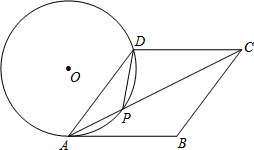 如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.
如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆. 如图,AB是⊙O的直径,弦BC=8,∠BOC=60°,OE⊥AC,垂足为E.
如图,AB是⊙O的直径,弦BC=8,∠BOC=60°,OE⊥AC,垂足为E.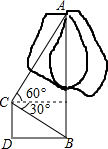 为申办2013年冬奥会,须改变某城市的交通状况,在街道拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区.现在某工人站在离B点3米远的D处,从C点测得树的顶端A点的仰角为60°,树的底部B点的俯角为30°.问:距离B点8米元的保护物是否存在危险?
为申办2013年冬奥会,须改变某城市的交通状况,在街道拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区.现在某工人站在离B点3米远的D处,从C点测得树的顶端A点的仰角为60°,树的底部B点的俯角为30°.问:距离B点8米元的保护物是否存在危险?