题目内容
7.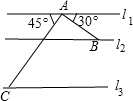 如图,三条平行的高速公路l1、l2、l3分别经过A、B、C三个城市,AB、AC分别为两条连接城市的普通公路,AB、AC分别与l1成30°、45°角,已知AB=200千米,AC=400千米,求两条高速公路l2、l3之间的距离(结果保留根号).
如图,三条平行的高速公路l1、l2、l3分别经过A、B、C三个城市,AB、AC分别为两条连接城市的普通公路,AB、AC分别与l1成30°、45°角,已知AB=200千米,AC=400千米,求两条高速公路l2、l3之间的距离(结果保留根号).
分析 过A作AD⊥l2于D,延长AD交l3于E,构成两个直角三角形,解两个直角三角形分别求得AD=100,AE=200$\sqrt{2}$,即可求得两条高速公路l2、l3之间的距离.
解答 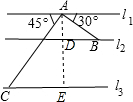 解:过A作AD⊥l2于D,延长AD交l3于E,
解:过A作AD⊥l2于D,延长AD交l3于E,
在RT△ABD中,∠ABD=30°,AB=200,
∴AD=100,
在RT△ACE中,∠ACE=45°,AC=400,
∵sin∠ACE=$\frac{AE}{AC}$,
∴AE=AC•sin45°=200$\sqrt{2}$,
∴DE=AE-DE=200$\sqrt{2}$-100,
答:两条高速公路l2、l3之间的距离为(200$\sqrt{2}$-100)千米.
点评 此题考查了解直角三角形的应用,主要是三角函数的基本概念及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
相关题目
15. 如图,A,B,C是⊙O上的三点,∠AOC=50°,则∠ABC的度数为( )
如图,A,B,C是⊙O上的三点,∠AOC=50°,则∠ABC的度数为( )
 如图,A,B,C是⊙O上的三点,∠AOC=50°,则∠ABC的度数为( )
如图,A,B,C是⊙O上的三点,∠AOC=50°,则∠ABC的度数为( )| A. | 20° | B. | 25° | C. | 35° | D. | 50° |
2. 图1是由6个小正方形组成的立体图形,它的左视图是( )
图1是由6个小正方形组成的立体图形,它的左视图是( )
 图1是由6个小正方形组成的立体图形,它的左视图是( )
图1是由6个小正方形组成的立体图形,它的左视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图,点E在直线CB上,点F在直线AD上,连接EF,且∠E=∠F,∠A=∠C,求证:AB∥CD.
如图,点E在直线CB上,点F在直线AD上,连接EF,且∠E=∠F,∠A=∠C,求证:AB∥CD.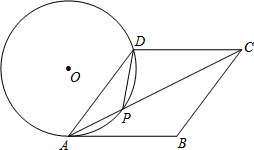 如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.
如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.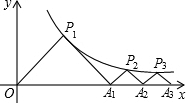 如图,点P1(x1,y1),点P2(x2,y2),P3(x3,y3)都在函数y=$\frac{k}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,都是等腰直角三角形,斜边OA3,A1A2,A2A3都在x轴上,已知点P1的坐标为(1,1),则点P3的坐标为($\sqrt{3}$+$\sqrt{2}$,$\sqrt{3}$-$\sqrt{2}$).
如图,点P1(x1,y1),点P2(x2,y2),P3(x3,y3)都在函数y=$\frac{k}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,都是等腰直角三角形,斜边OA3,A1A2,A2A3都在x轴上,已知点P1的坐标为(1,1),则点P3的坐标为($\sqrt{3}$+$\sqrt{2}$,$\sqrt{3}$-$\sqrt{2}$).