题目内容
4.在平面直角坐标系中,对点(x,y)的一次操作变换记为P1(x,y),定义其变换法则如下:P1(x,y)=(x+y,x-y),且规定Pn(x,y)=P1(Pn-1(x,y)),(n为大于1的整数).例如:P1(1,2)=(3,-1),P2(1,2)=P1(P1(1,2))=P1(3,-1)=(2,4),P3(1,2)=P1(P2(1,2))=P1(2,4)=(6,-2),则P2011(1,-1)=(0,21006).分析 根据题目中的新定义,可以算出Pn(1,-1)的前几项,然后观察,可以总结出横纵坐标的规律,从而可以解答本题.
解答 解:根据题目中的新定义可得:
P1(1,-1)=(0,2),
P2(1,-1)=(2,-2),
P3(1,-1)=(0,4),
P4(1,-1)=(4,-4),
P5(1,-1)=(0,8),
P6(1,-1)=(8,-8).
由上面可以发现当点Pn的右下角n为奇数时,横坐标都为0,纵坐标为${2}^{\frac{n+1}{2}}$;当点Pn的右下角n为偶数数时,横坐标都为${2}^{\frac{n}{2}}$,纵坐标都为-${2}^{\frac{n}{2}}$.
故${P}_{2011}(1,-1)=(0,{2}^{\frac{2011+1}{2}})$=(0,21006).
故答案为:(0,21006).
点评 本题考查规律性:点的坐标,解题的关键是先写出点Pn的前几项,能发现其中的规律.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.若x:y=1:3,则$\frac{2x+y}{x-y}$的值是( )
| A. | -5 | B. | -$\frac{5}{2}$ | C. | $\frac{5}{2}$ | D. | 5 |
9.为迎接国庆节,某班同学做了一些拉花布置教室,李丽搬来了高2.5米的梯子,准备把拉花挂到2.4米高的墙上,则梯子底端与墙角之间的距离应为( )
| A. | 0.7米 | B. | 0.8米 | C. | 0.9米 | D. | 1.0米 |
13.一元二次方程3x(1-x)+10=2(x+2)的二次项系数和常数项分别是( )
| A. | 3,6 | B. | 3,-1 | C. | -3,6 | D. | 3,1 |
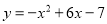 ,当
,当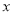 取值为
取值为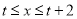 时,有最大值
时,有最大值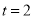 ,则
,则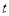 的取值范围为( )
的取值范围为( )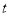 ≤0 B. 0≤
≤0 B. 0≤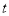 ≤3 C.
≤3 C. 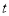 ≥3 D. 以上都不对
≥3 D. 以上都不对 如图,在△ABF与△CDE中,AB=CD,BF=DE,点A、E、F、C在同一条直线上,AE=CF,求证:△ABF≌△CDE.
如图,在△ABF与△CDE中,AB=CD,BF=DE,点A、E、F、C在同一条直线上,AE=CF,求证:△ABF≌△CDE. 如图,当太阳光与地面上的树影成45°角时,树影投射在墙上的影高CD等于2米,若树根到墙的距离BC等于8米,则树高AB等于10米.
如图,当太阳光与地面上的树影成45°角时,树影投射在墙上的影高CD等于2米,若树根到墙的距离BC等于8米,则树高AB等于10米.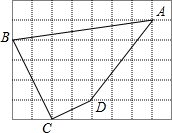 如图,每个小正方形的边长为1.
如图,每个小正方形的边长为1. 如图,△ABC中,∠A=60°.
如图,△ABC中,∠A=60°.