题目内容
16.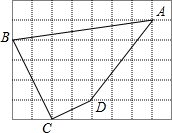 如图,每个小正方形的边长为1.
如图,每个小正方形的边长为1.(1)求四边形ABCD的面积和周长;
(2)∠BCD是直角吗?说明理由.
分析 (1)直接利用勾股定理得出各边长,进而利用四边形所在矩形面积减去周围三角形面积得出答案;
(2)利用勾股定理的逆定理得出答案.
解答 解:(1)由勾股定理可得:AB2=32+32=18,
则AB=$\sqrt{50}$=5$\sqrt{2}$,
∵BC2=42+22=20,
∴BC=2$\sqrt{5}$,
∵CD2=22+12=5,
∴CD=$\sqrt{5}$,
∵AD2=32+42=25,
∴AD=5,
故四边形ABCD的周长为:5$\sqrt{2}$+2$\sqrt{5}$+5+$\sqrt{5}$=5$\sqrt{2}$+3$\sqrt{5}$+5,
四边形ABCD的面积为:7×5-$\frac{1}{2}$(1×7+4×2+2×1+4×3)=35-14.5=20.5;
(2)由(1)得:BC2=20,CD2=5,而BD2=32+42=25,
故DC2+BC2=BD2,
则∠BCD=90°.
点评 此题主要考查了勾股定理以及其逆定理,正确应用勾股定理是解题关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
7.已知一次函数y=-5x+m的图象经过点(-2,7),则下列点在函数图象上的是( )
| A. | (0,-2) | B. | (1,8) | C. | (-3,12) | D. | (-1,1) |
3.一元二次方程x2-3x-5=0根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
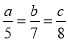 ,且3a-2b+c=3,则2a+4b-3c的值是( )
,且3a-2b+c=3,则2a+4b-3c的值是( )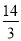
 如图,已知AB=AC,BD=DC,图中∠B和∠C相等吗?为什么?
如图,已知AB=AC,BD=DC,图中∠B和∠C相等吗?为什么?