题目内容
15．
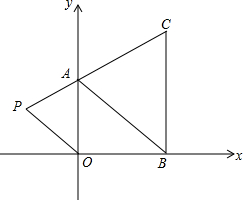如图，在下面直角坐标系中，已知A（0，2），B（3，0），C（3，4）三点，在第二象限内有一点P（m，$\frac{1}{2}$）．（1）如果请用含m的式子表示四边形ABOP的面积．
（2）m为何值时，四边形ABOP的面积与△ABC的面积相等？
分析 （1）直接利用三角形面积求法结合四边形ABOP的面积为：S△APO+S△AOB，即可得出答案；
（2）求出△ABC的面积进而得出等式求出答案．
解答 解：（1）四边形ABOP的面积为：S△APO+S△AOB=$\frac{1}{2}$×（-m）×2+$\frac{1}{2}$×2×3=-m+3；
（2）由点的坐标可得：S△ABC=$\frac{1}{2}$×4×3=6，
故6=-m+3，
解得：m=-3，
即m为-3时，四边形ABOP的面积与△ABC的面积相等．
点评 此题主要考查了坐标与图形的性质，正确求出相关三角形面积是解题关键．
练习册系列答案
相关题目
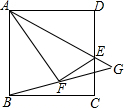如图，正方形ABCD中，E是CD的中点，连接AE，沿AE折叠，使得点D落在正方形内的点F处，连接BF并延长，交AE的延长线于点G．
根据如图所示的程序计算函数值，若输入的x的值为-$\frac{5}{2}$，则输出y的值为-2．
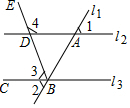如图所示，直线l1与l2，l3相交于A，B两点，∠ABC的平分线交l2于点D，已知∠1=∠2=62°．
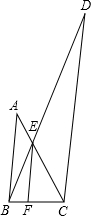如图，AB∥EF∥CD，已知AB=20，BC=10，CD=80，求EF的值．
如图，在?ABCD中，点E在边AD的延长线上，DE=AD，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$．