题目内容
17. 如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为8cm2或2$\sqrt{15}$cm2或2$\sqrt{7}$cm2.
如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为8cm2或2$\sqrt{15}$cm2或2$\sqrt{7}$cm2.
分析 因为等腰三角形腰的位置不明确,所以分三种情况进行讨论:
(1)△AEF为等腰直角三角形,直接利用面积公式求解即可;
(2)先利用勾股定理求出AE边上的高BF,再代入面积公式求解;
(3)先求出AE边上的高DF,再代入面积公式求解.
解答 解:分三种情况计算:
(1)当AE=AF=4时,如图:
∴S△AEF=$\frac{1}{2}$AE•AF=$\frac{1}{2}$×4×4=8(cm2);
(2)当AE=EF=4时,如图: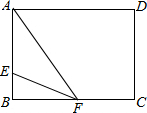
则BE=5-4=1,
BF=$\sqrt{E{F}^{2}-B{E}^{2}}$=$\sqrt{{4}^{2}-{1}^{2}}$=$\sqrt{15}$,
∴S△AEF=$\frac{1}{2}$•AE•BF=$\frac{1}{2}$×4×$\sqrt{15}$=2$\sqrt{15}$(cm2);
(3)当AE=EF=4时,如图:
则DE=7-4=3,
DF=$\sqrt{E{F}^{2}-D{E}^{2}}$=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,
∴S△AEF=$\frac{1}{2}$AE•DF=$\frac{1}{2}$×4×$\sqrt{7}$=2$\sqrt{7}$(cm2);
故答案为:8或2$\sqrt{15}$或2$\sqrt{7}$.
点评 本题主要考查矩形的角是直角的性质和勾股定理的运用,要根据三角形的腰长的不确定分情况讨论,有一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.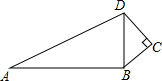 如图,己知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°,则AD=( )
如图,己知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°,则AD=( )
 如图,己知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°,则AD=( )
如图,己知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°,则AD=( )| A. | 10 | B. | 13 | C. | 8 | D. | 11 |
8.若一个菱形的两条对角线长分别是5cm和10cm,则与该菱形面积相等的正方形的边长是( )
| A. | 6cm | B. | 5cm | C. | $\sqrt{5}$cm | D. | 7.5cm |
12.若一组数据1、a、2、3、4的平均数与中位数相同,则a不可能是下列选项中的( )
| A. | 0 | B. | 2.5 | C. | 3 | D. | 5 |
 将一列数$-1,\frac{1}{2},-\frac{1}{3},\frac{1}{4},-\frac{1}{5},\frac{1}{6},…$按一定的规律排,如右表.按此规律排下去,第200行第100个数为$\frac{1}{20200}$.
将一列数$-1,\frac{1}{2},-\frac{1}{3},\frac{1}{4},-\frac{1}{5},\frac{1}{6},…$按一定的规律排,如右表.按此规律排下去,第200行第100个数为$\frac{1}{20200}$.


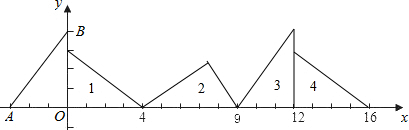
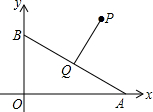 如图,点A、B分别在x轴和y轴的正半轴上运动,在运动过程中保持AB=4不变,点Q为AB的中点,已知点P的坐标为(4,3),连结PQ,则PQ长的最小值是3.
如图,点A、B分别在x轴和y轴的正半轴上运动,在运动过程中保持AB=4不变,点Q为AB的中点,已知点P的坐标为(4,3),连结PQ,则PQ长的最小值是3.