题目内容
6.根据指令(S,A)(说明:S≥0,单位:厘米;0°≤A<180°),机器人在平面上能完成下列动作:先原地逆时针旋转角度A,再朝其面对的方向沿直线行走距离S.若现在机器人在平面直角坐标系的坐标原点处,且面对x轴正方向.若机器人下一个指令(4,60°),则机器人应移动到点(2,2$\sqrt{3}$).分析 设此点为A,作AB⊥x轴于点B,根据旋转的性质得到OA=4,∠AOB=60°,解直角三角形即可得到结论.
解答  解:设此点为A,作AB⊥x轴于点B,则OA=4,∠AOB=60°,
解:设此点为A,作AB⊥x轴于点B,则OA=4,∠AOB=60°,
∴OB=AO×cos60°=2,AB=AO×sin60°=2$\sqrt{3}$,
∴机器人应移动到点(2,2$\sqrt{3}$),
故答案为:(2,2$\sqrt{3}$).
点评 本题考查了坐标与图形变化-旋转,求新定义下的点的旋转坐标,应理解运动指令的含义,构造直角三角形求解是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 国旗法对国旗的构成由明确的规定,国旗应为长方形,长与宽的比为3:2,某学校所使用的国旗正是按这一比例制作的,长为2.4m.已知学校的旗杆高为10m,在无风的天气里,国旗会自然下垂,求国旗下垂时最低处离地面的距离是多少?(结果保留一位小数,$\sqrt{13}$≈3.6)
国旗法对国旗的构成由明确的规定,国旗应为长方形,长与宽的比为3:2,某学校所使用的国旗正是按这一比例制作的,长为2.4m.已知学校的旗杆高为10m,在无风的天气里,国旗会自然下垂,求国旗下垂时最低处离地面的距离是多少?(结果保留一位小数,$\sqrt{13}$≈3.6) 将一列数$-1,\frac{1}{2},-\frac{1}{3},\frac{1}{4},-\frac{1}{5},\frac{1}{6},…$按一定的规律排,如右表.按此规律排下去,第200行第100个数为$\frac{1}{20200}$.
将一列数$-1,\frac{1}{2},-\frac{1}{3},\frac{1}{4},-\frac{1}{5},\frac{1}{6},…$按一定的规律排,如右表.按此规律排下去,第200行第100个数为$\frac{1}{20200}$.


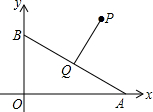 如图,点A、B分别在x轴和y轴的正半轴上运动,在运动过程中保持AB=4不变,点Q为AB的中点,已知点P的坐标为(4,3),连结PQ,则PQ长的最小值是3.
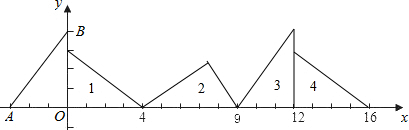
如图,点A、B分别在x轴和y轴的正半轴上运动,在运动过程中保持AB=4不变,点Q为AB的中点,已知点P的坐标为(4,3),连结PQ,则PQ长的最小值是3.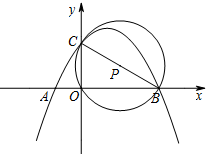 如图,抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,$\sqrt{3}$)三点.
如图,抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,$\sqrt{3}$)三点. 如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的$\frac{1}{3}$,另一根露出水面的长度是它的$\frac{1}{5}$,两根铁棒长度之和为220cm,此时木桶中水的深度是80cm.
如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的$\frac{1}{3}$,另一根露出水面的长度是它的$\frac{1}{5}$,两根铁棒长度之和为220cm,此时木桶中水的深度是80cm.