题目内容
3. 如图,等边△ABC中,BC=6,D、E分别在BC、AC上,且DE∥AC,MN是△BDE的中位线.将线段DE从BD=2处开始向AC平移,当点D与点C重合时停止运动,则在运动过程中线段MN所扫过的区域面积为2$\sqrt{3}$.
如图,等边△ABC中,BC=6,D、E分别在BC、AC上,且DE∥AC,MN是△BDE的中位线.将线段DE从BD=2处开始向AC平移,当点D与点C重合时停止运动,则在运动过程中线段MN所扫过的区域面积为2$\sqrt{3}$.
分析 因为MN是三角形EMN的中位线,所以MN∥BD,所以在运动过程中线段MN所扫过的区域为梯形,然后分别求得梯形的上底、下底和高,然后利用公式计算即可.
解答 解:在运动过程中线段MN所扫过的区域面积如图阴影所示: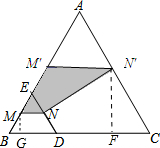
∵MN是△BDE的中位线.
∴MN=$\frac{1}{2}BD$=$\frac{1}{2}×2$=1,且MN∥BD.
同理:M′N′=3,且M′N′∥BD
∴四边形MNN′M′为梯形.
MG=MB•sin30°=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
N′F=N′C•sin30°=3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$.
∴梯形MNN′M′的高=$\frac{3\sqrt{3}}{2}-\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
∴梯形MNN′M′的面积=$\frac{1}{2}(MN+M′N′)$(FN-MG)
=$\frac{1}{2}$×$4×\sqrt{3}$
=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题主要考查轨迹的问题,由三角形中位线的性质判断出MN扫过的区域的形状是解题的关键.

练习册系列答案
相关题目



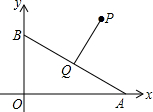 如图,点A、B分别在x轴和y轴的正半轴上运动,在运动过程中保持AB=4不变,点Q为AB的中点,已知点P的坐标为(4,3),连结PQ,则PQ长的最小值是3.
如图,点A、B分别在x轴和y轴的正半轴上运动,在运动过程中保持AB=4不变,点Q为AB的中点,已知点P的坐标为(4,3),连结PQ,则PQ长的最小值是3.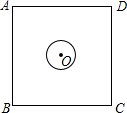 如图,圆心O恰好为正方形ABCD的中心,已知AB=10,⊙O的半径为1,现将⊙O在正方形内部沿某一方向平移,当它与正方形ABCD的某条边相切时停止平移,设此时的平移的距离为d,则d的取值范围是4≤d$≤4\sqrt{2}$.
如图,圆心O恰好为正方形ABCD的中心,已知AB=10,⊙O的半径为1,现将⊙O在正方形内部沿某一方向平移,当它与正方形ABCD的某条边相切时停止平移,设此时的平移的距离为d,则d的取值范围是4≤d$≤4\sqrt{2}$.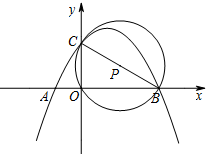 如图,抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,$\sqrt{3}$)三点.
如图,抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,$\sqrt{3}$)三点. 如图,矩形OABC在平面直角坐标系中,点B的坐标为(4,3),直线l:y=-2x+b经过点A交x轴于点G.
如图,矩形OABC在平面直角坐标系中,点B的坐标为(4,3),直线l:y=-2x+b经过点A交x轴于点G.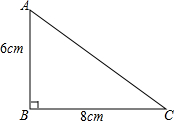 如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A出发,以1cm/s的速度沿AB边向点B移动,以此同时,点Q从点C出发,以2cm/s的速度沿CB边向点B移动,如果P,Q同时出发,经过几秒,△PBQ的面积等于8cm2?
如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A出发,以1cm/s的速度沿AB边向点B移动,以此同时,点Q从点C出发,以2cm/s的速度沿CB边向点B移动,如果P,Q同时出发,经过几秒,△PBQ的面积等于8cm2?