题目内容
过△ABC的顶点C作边AB的垂线将∠ACB分为20°和40°的两个角，那么∠A，∠B中较大的角的度数是____________．
70°
【解析】根据题意画出图形，则∠ACD=40°，∠DCB=20°.
∵CD⊥AB，∠ACD=40°，∠DCB=20°，
∴∠A=50°，∠B=70°，
∴∠A、∠B中较大的角的度数是70°.
故答案为：70°.
口算题天天练系列答案如图，在平面直角坐标系中，四边形OBCD是边长为4的正方形，平行于对角线BD的直线l从O出发，沿x轴正方向以每秒1个单位长度的速度运动，运动到直线l与正方形没有交点为止．设直线l扫过正方形OBCD的面积为S，直线l运动的时间为t(秒)，下列能反映S与t之间函数关系的图象是( )
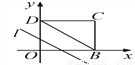
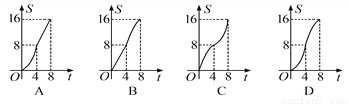
A. A B. B C. C D. D
D
【解析】试题分析：根据三角形的面积即可求出S与t的函数关系式，根据函数关系式选择图象．
试题解析：如图：
①当0≤t≤4时，S=×t×t=t2，即S=t2．
该函数图象是开口向上的抛物线的一部分．
故B、C错误；
②当4＜t≤8时，S=16-×（8-t）×（8-t）=-t2+8t-16．
该函数图象是开口向下的抛物线的一部分．
故A错误．
... 如图所示是二次函数y=ax2﹣x+a2﹣1的图象，则a的值是（ ）
A. a=﹣1 B. a=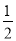
C. a=1 D. a=1或a=﹣1
C
【解析】由图象得，此二次函数过原点（0，0），
把点（0，0）代入函数解析式得a2-1=0，解得a=±1；
又因为此二次函数的开口向上，所以a＞0；
所以a=1．
故选C． 已知：如图，点C在线段AB上，以AC和BC为边在AB的同侧作正三角形△ACM和△BCN，连结AN、BM，分别交CM、CN于点P、Q．求证：PQ∥AB．
见解析
【解析】试题分析：首先证明△ACN≌△MCB可得∠ANC=∠MBC，再证明△PCN≌△QCB可得PC=QC，再有∠MCN=60°可得△PCQ是等边三角形，进而得到∠PQC=60°，可证明PQ∥AB．
试题解析：∵△ACM和△BCN都是正三角形，
∴∠ACM=∠BCN=60°，AC=CM，BC=CN.
∵点C在线段AB上，
∴∠ACM=∠BCN=∠MCN=60°... 如图，△ABC中，∠C＝90°，CD⊥AB，CM平分AB，CE平分∠DCM，则∠ACE的度数是______．
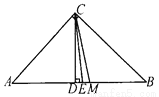
45°
【解析】∵△ABC中,∠C=90°，
∴∠A+∠B=90°，
∵CD⊥AB，
∴∠ADC=90°，
∴∠A+∠ACD=90°，
∴∠ACD=∠B，
∵CM平分AB，
∴AM=BM=CM，
∴∠BCM=∠B，
∴∠BCM=∠ACD，
∵CE平分∠DCM，
∴∠DCE=∠MCE，
∴∠ACD+∠DCE=∠BCM+∠M... 已知等腰三角形的一个角为75°，则其顶角为（ ）.
A. 30° B. 75° C. 105° D. 30°或75°
D
【解析】试题分析：因为等腰三角形的一个角为75°，没有明确说明是底角还是顶角，所以要分两种情况进行分析．
【解析】
当75°角为底角时，顶角为180°﹣75°×2=30°；
75°角为顶角时，其底角==52.5°，
所以其顶角为30°或75°．
故选D． 一个钝角三角形的三条角平分线所在的直线一定交于一点，这交点一定在( )
A. 三角形内部 B. 三角形的一边上 C. 三角形外部 D. 三角形的某个顶点上
A
【解析】三角形三条角平分线所在的直线一定交于一点，这一点是三角形的内心即内切圆的圆心，此点在三角形（锐角三角形、直角三角形、钝角三角形）内部.
故选：A. 二次函数y=ax2+bx+c的图象过A（﹣3，0），B（1，0），C（0，3），点D在函数图象上，点C，D是二次函数图象上的一对对称点，一次函数图象过点B，D，求：
（1）一次函数和二次函数的解析式；
（2）写出使一次函数值大于二次函数值的x的取值范围．
（1）y1=﹣x2﹣2x+3（2）x＜﹣2或x＞1．
【解析】
试题分析：（1）将A、B、C的坐标代入抛物线的解析式中即可求得二次函数的解析式，进而可根据抛物线的对称轴求出D点的坐标，再用待定系数法求出一次函数解析式；
（2）根据（1）画出函数图象，即可写出一次函数值大于二次函数值的x的取值范围．
【解析】
（1）二次函数y1=ax2+bx+c的图象经过点A（﹣3，0），... （2016四川省泸州市）某商店购买60件A商品和30件B商品共用了1080元，购买50件A商品和20件B商品共用了880元．
（1）A、B两种商品的单价分别是多少元？
（2）已知该商店购买B商品的件数比购买A商品的件数的2倍少4件，如果需要购买A、B两种商品的总件数不少于32件，且该商店购买的A、B两种商品的总费用不超过296元，那么该商店有哪几种购买方案？
（1）A种商品的单价为16元、B种商品的单价为4元；（2）有两种方案：方案（1）：m=12，2m﹣4=20 即购买A商品的件数为12件，则购买B商品的件数为20件；方案（2）：m=13，2m﹣4=22 即购买A商品的件数为13件，则购买B商品的件数为22件．
【解析】试题分析：(1)、设A种商品的单价为x元、B种商品的单价为y元，根据题意得出方程组，从而求出x和y的值；(2)、设购买A商品的...