在△ABC中.BC=54.CA=45.AB=63.另一个和它相似的三角形的最短边为15.则最长边一定是( )A．18B．21C．24D．19.5 题目和参考答案——青夏教育精英家教网—

题目内容

6．在△ABC中，BC=54，CA=45，AB=63，另一个和它相似的三角形的最短边为15，则最长边一定是（　　）

A．

B．

C．

D．

19.5

分析根据相似三角形的性质得出关于x的方程，求出方程的解即可．

解答解：设三角形的最长边为x，
∵在△ABC中，BC=54，CA=45，AB=63，另一个和它相似的三角形的最短边为15，
∴$\frac{63}{x}$=$\frac{45}{15}$，
解得：x=21，
故选B．

点评本题考查了相似三角形的性质的应用，能根据相似三角形的性质得出方程是解此题的关键，注意：相似三角形的对应边的比相等．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

16．

如图，抛物线y=-$\frac{5}{4}$x²+bx+c与y轴交于点A（0，1），过点A的直线与抛物线交于另一点B（3，$\frac{5}{2}$），过点B作BC⊥x轴，垂足为C．点P是x轴正半轴上的一动点，过点P作PN⊥x轴，交直线AB于点M，交抛物线于点N，设OP的长度为m．
（1）求抛物线的解析式；
（2）当点P在线段OC上（不与点O、C重合）时，试用含m的代数式表示线段PM的长度；
（3）连结CM，BN，当m为何值时，以B、C、M、N为顶点的四边形为平行四边形？

17．

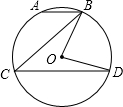如图所示，在圆O中弦AB∥CD，若∠ABC=50°，则∠BOD等于（　　）

14．

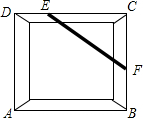如图，利用所学的知识进行逻辑推理，工人盖房时常用木条EF固定矩形门框ABCD，使其不变形这种做法的根据是（　　）

	A．	两点之间线段最短		B．	矩形的对称性
	C．	矩形的四个角都是直角		D．	三角形的稳定性

1．若△AED∽△ABC，AD=6cm，AC=12cm，则△AED与△ABC的相似比为1：2．

11．△ABC的三边长分别为6，8，12，△A₁B₁C₁的三边长分别为2，3，2.5，△A₂B₂C₂的三边长分别为6，3，4，则△ABC与△A₂B₂C₂相似．

18．对于方程3x²-x-2=0，下列判断正确的是（　　）

15．（1）比较下列两个数的大小：4＞$\sqrt{15}$；
（2）$\sqrt{15}$在哪两个连续整数之间？$\sqrt{15}$的整数部分是多少？
（3）若5-$\sqrt{15}$的整数部分是a，小数部分是b，试求a，b的值．

16．一个三角形三边长的比为3：4：5，它的周长是24cm，这个三角形的面积为24cm²．

试题分类