题目内容
16．一个三角形三边长的比为3：4：5，它的周长是24cm，这个三角形的面积为24cm2．分析 首先设三边长为3xcm，4xcm，5xcm，根据勾股定理逆定理可证出∠C=90°，根据周长为24cm可得3x+4x+5x=24，再解可得x的值，进而可得两直角边长，然后再计算出面积即可．
解答 
解：设三边长为3xcm，4xcm，5xcm，
∵（3x）2+（4x）2=（5x）2，
∴AC2+BC2=AB2，
∴∠C=90°，
∵周长为24cm，
∴3x+4x+5x=24，
解得：x=2，
∴3x=6，4x=8，
∴它的面积为：$\frac{1}{2}$×6×8=24（cm2），
故答案为：24．
点评 此题主要考查了勾股定理逆定理，关键是掌握两边的平方和等于第三边的平方，这个三角形是直角三角形．
练习册系列答案
名校课堂系列答案
相关题目
6．在△ABC中，BC=54，CA=45，AB=63，另一个和它相似的三角形的最短边为15，则最长边一定是（ ）
| A． | 18 | B． | 21 | C． | 24 | D． | 19.5 |
如图，圆中有一条直径，三条弦，圆中以A为一个端点的优弧有四条，劣弧有四条．
4．在⊙O与⊙O′中，若∠AOB=∠A′O′B′，则AB与A′B′的关系为（ ）
| A． | AB=A′B′ | B． | AB＞A′B′ | C． | AB＜A′B′ | D． | 无法确定 |
11．
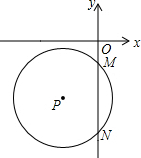如图，半径为5的⊙P与y轴交于点M（0，-4），N（0，-10），函数y=kx的图象经过点P，则k的值为（ ）
如图，半径为5的⊙P与y轴交于点M（0，-4），N（0，-10），函数y=kx的图象经过点P，则k的值为（ ）| A． | -$\frac{4}{7}$ | B． | -$\frac{7}{4}$ | C． | $\frac{4}{7}$ | D． | $\frac{7}{4}$ |
5．小明沿着坡度为1：2的山坡向上走了1 000m，则他升高了（ ）
| A． | 200$\sqrt{5}$m | B． | 500m | C． | 500$\sqrt{3}$m | D． | 1000m |
