题目内容
15.(1)比较下列两个数的大小:4>$\sqrt{15}$;(2)$\sqrt{15}$在哪两个连续整数之间?$\sqrt{15}$的整数部分是多少?
(3)若5-$\sqrt{15}$的整数部分是a,小数部分是b,试求a,b的值.
分析 (1)根据算术平方根得出4=$\sqrt{16}$,即可得出答案;
(2)先估算出$\sqrt{15}$的范围,即可得出答案;
(3)先估算出$\sqrt{15}$的范围,再求出5-$\sqrt{15}$的范围,即可得出答案.
解答 解:(1)∵4=$\sqrt{16}$,
∴4$>\sqrt{15}$,
故答案为:>;
(2)∵3<$\sqrt{15}$<4,
∴$\sqrt{15}$在整数3和4之间,$\sqrt{15}$的整数部分是3;
(3)∵3<$\sqrt{15}$<4,
∴-3>-$\sqrt{15}$>-4,
∴2>5-$\sqrt{15}$>1,
∴a=1,b=5-$\sqrt{15}$-1=4-$\sqrt{15}$.
点评 本题考查了估算无理数大小的应用,能估算出$\sqrt{15}$的范围是解此题的关键,难度不大.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
6.在△ABC中,BC=54,CA=45,AB=63,另一个和它相似的三角形的最短边为15,则最长边一定是( )
| A. | 18 | B. | 21 | C. | 24 | D. | 19.5 |
10.一个两位数,个位上的数字比十位上的数字小4,且个位数字与十位数字的平方和比这个两位数小4,若设个位数字为a,则可列方程为( )
| A. | a2(a-4)2=10(a-4)+a-4 | B. | a2+(a+4)2=10a+a-4-4 | ||
| C. | a2+(a+4)2=10(a+4)+a-4 | D. | a2+(a-4)2=10a+(a-4)-4 |
20.下列各式中$\sqrt{15}$,$\sqrt{3a}$,$\sqrt{{6}^{2}-1}$,$\sqrt{{a}^{2}+{b}^{2}}$,$\sqrt{{m}^{2}+20}$,$\sqrt{-144}$,二次根式的个数有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
4.在⊙O与⊙O′中,若∠AOB=∠A′O′B′,则AB与A′B′的关系为( )
| A. | AB=A′B′ | B. | AB>A′B′ | C. | AB<A′B′ | D. | 无法确定 |
5.小明沿着坡度为1:2的山坡向上走了1 000m,则他升高了( )
| A. | 200$\sqrt{5}$m | B. | 500m | C. | 500$\sqrt{3}$m | D. | 1000m |
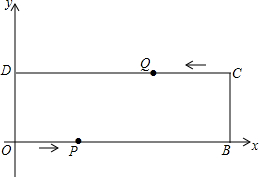 已知长方形的生活小区OBCD的边长分别为40米和130米,如图,建立平面直角坐标系,“创文明城市”宣传车点P从点O出发,沿OB运动至点B停止,宣传车点Q从点C出发,沿CD运动至点D停止,两车同时出发,速度都是1米/秒;宣传车音响半径可达25米,(两点间距离公式:|AB|=$\sqrt{({x}_{A}-{x}_{B})^{2}+({y}_{A}-{y}_{B})^{2}}$)
已知长方形的生活小区OBCD的边长分别为40米和130米,如图,建立平面直角坐标系,“创文明城市”宣传车点P从点O出发,沿OB运动至点B停止,宣传车点Q从点C出发,沿CD运动至点D停止,两车同时出发,速度都是1米/秒;宣传车音响半径可达25米,(两点间距离公式:|AB|=$\sqrt{({x}_{A}-{x}_{B})^{2}+({y}_{A}-{y}_{B})^{2}}$) 如图,圆中有一条直径,三条弦,圆中以A为一个端点的优弧有四条,劣弧有四条.
如图,圆中有一条直径,三条弦,圆中以A为一个端点的优弧有四条,劣弧有四条.