题目内容
2. 如图,已知Rt△ABC中,∠C=90°,点D、E分别是AB、AC边的中点,BC=6,AC=8,将线段DE沿水平方向平移,使点E落在CB上,则平移的距离为( )
如图,已知Rt△ABC中,∠C=90°,点D、E分别是AB、AC边的中点,BC=6,AC=8,将线段DE沿水平方向平移,使点E落在CB上,则平移的距离为( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
分析 由勾股定理求出AB,由三角形中位线定理得出DE=$\frac{1}{2}$BC=3,将线段DE沿水平方向平移,使点E落在CB,则E成为BC的中点,即可得出结论.
解答 解:Rt△ABC中,∠C=90°,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵点D、E分别是AB、AC边的中点,
∴DE=$\frac{1}{2}$BC=3,将线段DE沿水平方向平移,使点E落在CB上,
则平移的距离=BD=$\frac{1}{2}$AB=5;
故选:A.
点评 本题考查了勾股定理、三角形中位线定理以及平移的性质;熟练掌握勾股定理和三角形中位线定理是解决问题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
17.-2017的相反数是( )
| A. | -2017 | B. | -$\frac{1}{2017}$ | C. | $\frac{1}{2017}$ | D. | 2017 |
11.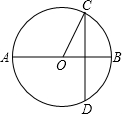 如图,AB是⊙O的直径,弦CD⊥AB,∠OCD=30°,CD=2$\sqrt{3}$,则扇形BOC的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠OCD=30°,CD=2$\sqrt{3}$,则扇形BOC的面积为( )
 如图,AB是⊙O的直径,弦CD⊥AB,∠OCD=30°,CD=2$\sqrt{3}$,则扇形BOC的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠OCD=30°,CD=2$\sqrt{3}$,则扇形BOC的面积为( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | π | D. | 2π |
