题目内容
6.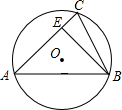 已知⊙O的直径为$\sqrt{5}$,锐角△ABC内接于⊙O,且AB=2,BE⊥AC于E,则sin∠CBE=$\frac{\sqrt{5}}{5}$.
已知⊙O的直径为$\sqrt{5}$,锐角△ABC内接于⊙O,且AB=2,BE⊥AC于E,则sin∠CBE=$\frac{\sqrt{5}}{5}$.
分析 连接OA、OB,由于OM⊥AB,根据垂径定理易证得∠BOM=$\frac{1}{2}$∠AOB,而由圆周角定理可得∠BCE=$\frac{1}{2}$∠AOB=∠BOM,因此∠CBE=∠OBM,只需求得∠OBM的正弦值即可;在Rt△OBM中,由垂径定理可得BM=1,已知⊙O的半径OB=$\frac{\sqrt{5}}{2}$,由勾股定理可求得OM,即可求出∠OBM即∠CBE的正弦值,由此得解.
解答 解:连接OA、OB,作OM⊥AB,
∵OM⊥AB,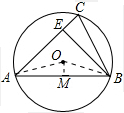
∴AM=BM=1,∠BOM=$\frac{1}{2}$∠AOB,
∵∠BCE=$\frac{1}{2}$∠AOB,
∴∠BCE=∠BOM,
∵BE⊥AC,
∴∠CBE=∠OBM,
在Rt△OBM中,OB=$\frac{\sqrt{5}}{2}$,
OM=$\sqrt{{OB}^{2}{-BM}^{2}}$=$\sqrt{{(\frac{\sqrt{5}}{2})}^{2}{-1}^{2}}$=$\frac{1}{2}$
∴sin∠OBM=sin∠CBE=$\frac{OM}{OB}$=$\frac{\sqrt{5}}{5}$;
故答案为$\frac{\sqrt{5}}{5}$.
点评 本题主要考查了垂径定理、圆周角定理、勾股定理的综合应用能力,能够根据已知条件找到∠CBE=∠OBM,是解决问题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
14.计算(-$\frac{4}{15}$)÷$\frac{2}{3}$×cos60°-2015°的结果是( )
| A. | $\frac{6}{5}$ | B. | ?-$\frac{6}{5}$ | C. | $\frac{4}{5}$ | D. | ?-$\frac{4}{5}$ |
1.下列说法正确的是( )
| A. | 同圆或等圆中弧相等,则它们所对的圆心角也相等 | |
| B. | 90°的圆心角所对的弦是直径 | |
| C. | 平分弦的直径垂直于这条弦 | |
| D. | 三点确定一个圆 |
11.下列运算正确的是( )
| A. | (-a2)2=-a4 | B. | $\sqrt{3}$+$\sqrt{4}$=2$\sqrt{3}$ | C. | (π-2)0=0 | D. | ($\frac{1}{3}$)-2=9 |
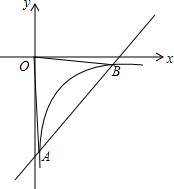 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于点A(1,-4)、点B(3,n).
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于点A(1,-4)、点B(3,n).