题目内容
17.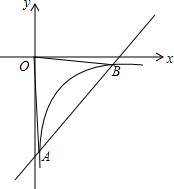 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于点A(1,-4)、点B(3,n).
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于点A(1,-4)、点B(3,n).(1)求此一次函数和反比例函数的解析式;
(2)求△AOB的面积.
分析 (1)先根据点A求出m值,再根据反比例函数解析式求出n值,利用待定系数法求一次函数的解析式;
(2)利用三角形的面积差求解.S△AOB=S△AOC-S△BOC=8-$\frac{8}{3}$=$\frac{16}{3}$.
解答 解:(1)将点A(1,-4)代入y=$\frac{m}{x}$中,-4=$\frac{m}{1}$,
∴m=-4
∴反比例函数解析式为y=-$\frac{4}{x}$,
将B(3,n)代入y=-$\frac{4}{x}$中,n=-$\frac{4}{3}$,
∴B点坐标为(3,-$\frac{4}{3}$),
将A(1,-4)、B(3,-$\frac{4}{3}$)的坐标分别代入y=kx+b中,得$\left\{\begin{array}{l}{k+b=-4}\\{3k+b=-\frac{4}{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=-\frac{16}{3}}\end{array}\right.$
∴一次函数的解析式为y=$\frac{4}{3}$x-$\frac{16}{3}$;
(2)设一次函数解析式图象与x轴交与点C,当y=0时,$\frac{4}{3}$x-$\frac{16}{3}$=0,
解得x=4,
∴C点坐标(4,0),
∴OC=4,
S△AOC=$\frac{1}{2}$•OC•|yA|=$\frac{1}{2}$×4×4=8,S△BOC=$\frac{1}{2}$•OC•|yB|=$\frac{1}{2}$×4×$\frac{4}{3}$=$\frac{8}{3}$,
S△AOB=S△AOC-S△BOC=8-$\frac{8}{3}$=$\frac{16}{3}$.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式.

| A. | -3 | B. | ±3 | C. | 3 | D. | -$\frac{1}{3}$ |
| A. | x<1 | B. | x≠1 | C. | x≥1 | D. | x≤1 |
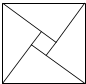 四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为1,大正方形面积为13,直角三角形的两条直角边为a、b,那么(a+b)2的值是25.
四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为1,大正方形面积为13,直角三角形的两条直角边为a、b,那么(a+b)2的值是25.
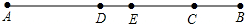 如图所示,线段AB=8cm,E为线段AB的中点,点C为线段EB上一点,且EC=3cm,点D为线段AC的中点,求线段DE的长度.
如图所示,线段AB=8cm,E为线段AB的中点,点C为线段EB上一点,且EC=3cm,点D为线段AC的中点,求线段DE的长度.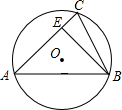 已知⊙O的直径为$\sqrt{5}$,锐角△ABC内接于⊙O,且AB=2,BE⊥AC于E,则sin∠CBE=$\frac{\sqrt{5}}{5}$.
已知⊙O的直径为$\sqrt{5}$,锐角△ABC内接于⊙O,且AB=2,BE⊥AC于E,则sin∠CBE=$\frac{\sqrt{5}}{5}$.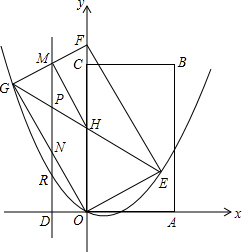 如图,矩形OABC的顶点A(2,0),C(0,2$\sqrt{3}$),将矩形OABC绕点O逆时针旋转30°,得矩形OEFG,线段GE、FO相交于点H,平行于y轴的直线MN分别交线段FG,GH,GO和x轴于点M,P,N,D,连结MH
如图,矩形OABC的顶点A(2,0),C(0,2$\sqrt{3}$),将矩形OABC绕点O逆时针旋转30°,得矩形OEFG,线段GE、FO相交于点H,平行于y轴的直线MN分别交线段FG,GH,GO和x轴于点M,P,N,D,连结MH