题目内容
8.若方程(x-3)2+a=0有实数根,则a的取值范围是( )| A. | a≤0 | B. | a≥0 | C. | a≠0 | D. | a为任意实数 |
分析 由方程有实数根,确定出a的范围即可.
解答 解:∵方程(x-3)2+a=0,即(x-3)2=-a有实数根有实数根,
∴-a≥0,即a≤0.
故选A.
点评 此题考查了解一元二次方程-直接开平方法,熟练掌握平方根定义是解本题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
19.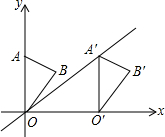 如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点在直线y=$\frac{2}{3}$x上一点,则点B与其对应点B′间的距离为( )
如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点在直线y=$\frac{2}{3}$x上一点,则点B与其对应点B′间的距离为( )
 如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点在直线y=$\frac{2}{3}$x上一点,则点B与其对应点B′间的距离为( )
如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点在直线y=$\frac{2}{3}$x上一点,则点B与其对应点B′间的距离为( )| A. | $\frac{2}{3}$ | B. | $\frac{9}{2}$ | C. | 3 | D. | 5 |
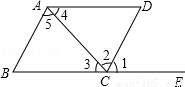
3. 如图,已知∠A=∠D,∠1=∠2,下列哪个条件不能得到△ABC≌△DEF( )
如图,已知∠A=∠D,∠1=∠2,下列哪个条件不能得到△ABC≌△DEF( )
 如图,已知∠A=∠D,∠1=∠2,下列哪个条件不能得到△ABC≌△DEF( )
如图,已知∠A=∠D,∠1=∠2,下列哪个条件不能得到△ABC≌△DEF( )| A. | ∠A=∠B | B. | BC=EF | C. | AB=DE | D. | CD=AF |
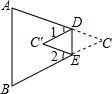 如图,在△ABC中,将∠C沿DE折叠,使顶点C落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=40°,则∠2的度数为40°.
如图,在△ABC中,将∠C沿DE折叠,使顶点C落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=40°,则∠2的度数为40°. 如图,在△ABC中,AB=6cm,AC=5cm,∠ABC与∠ACB的平分线相交于点O,过点O作DE∥BC,分别交AB,AC于点D,E,则△ADE的周长=11cm.
如图,在△ABC中,AB=6cm,AC=5cm,∠ABC与∠ACB的平分线相交于点O,过点O作DE∥BC,分别交AB,AC于点D,E,则△ADE的周长=11cm.