题目内容
20. 如图,在△ABC中,AB=6cm,AC=5cm,∠ABC与∠ACB的平分线相交于点O,过点O作DE∥BC,分别交AB,AC于点D,E,则△ADE的周长=11cm.
如图,在△ABC中,AB=6cm,AC=5cm,∠ABC与∠ACB的平分线相交于点O,过点O作DE∥BC,分别交AB,AC于点D,E,则△ADE的周长=11cm.
分析 根据角平分线的性质,可得∠DBO与∠OBC的关系,∠ECO与∠OCB的关系,根据平行线的性质,可得∠DOB与∠BOC的关系,∠EOC与∠OCB的关系,根据等腰三角形的判定,可得OD与BD的关系,OE与CE的关系,根据三角形的周长公式,可得答案.
解答 解:由∠ABC与∠ACB的平分线相交于点O,得
∠DBO=∠OBC,∠ECO=∠OCB.
由DE∥BC,得
∠DOB=∠BOC,∠EOC=∠OCB,
∠DOB=∠DBO,∠EOC=∠ECO,
∴DO=BD,OE=EC.
C△ADE=AD+DE+AE=AD+BD+AE+CE=AB+AC=11cm.
故答案为:11.
点评 本题考查了等腰三角形的判定与性质,利用等腰三角形的判定与性质是解题关键,又利用了角平分线的性质,平行线的性质.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
10.掷一颗均匀的骰子(正方体,各面标1-6这6个数字),6点朝上的概率为( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{1}{6}$ |
8.若方程(x-3)2+a=0有实数根,则a的取值范围是( )
| A. | a≤0 | B. | a≥0 | C. | a≠0 | D. | a为任意实数 |
15.若m<1,则(m-1)x>1-m的解集为( )
| A. | x>1 | B. | x<1 | C. | x<-1 | D. | x>-1 |
11.方程x(x+3)=x+3的根是( )
| A. | x=-3 | B. | x1=1,x2=-3 | C. | x1=3,x2=0 | D. | x1=0,x2=3 |
6.在Rt△ABC中,AD是斜边BC上的高,若CB=a,∠B=β,则AD等于( )
| A. | asin2β | B. | acos2β | C. | asinβcosβ | D. | asinβtanββ |
 如图,已知△ABD≌△CDB,且∠ABD=40°,∠CBD=20°,则∠A的度数为120°.
如图,已知△ABD≌△CDB,且∠ABD=40°,∠CBD=20°,则∠A的度数为120°.
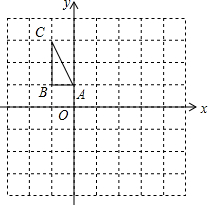 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3).
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3).