题目内容
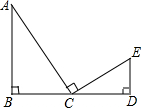如图，已知AB⊥BD，ED⊥BD，C是线段BD的中点，且AC⊥CE，∠A=30°，那么∠E=
考点：直角三角形的性质
专题：
分析：根据直角三角形两锐角互余求出∠ACB，再根据同角的余角相等求出∠E=∠ACB，从而得解．
解答：解：∵AB⊥BD，
∴∠ACB=90°-∠A=90°-30°=60°，
∵ED⊥BD，AC⊥CE，
∴∠ACB+∠DCE=90°，
∠DCE+∠E=90°，
∴∠E=∠ACB=60°．
故答案为：60°．
∴∠ACB=90°-∠A=90°-30°=60°，
∵ED⊥BD，AC⊥CE，
∴∠ACB+∠DCE=90°，
∠DCE+∠E=90°，
∴∠E=∠ACB=60°．
故答案为：60°．
点评：本题考查了直角三角形的性质，同角的余角相等的性质，熟记性质是解题的关键．
练习册系列答案
培优口算题卡系列答案
相关题目
702班某兴趣小组有7名成员，他们的年龄（单位：岁）分别为：12，13，13，14，12，13，15，则他们年龄的众数和中位数分别为（ ）
| A、13，14 |
| B、14，13 |
| C、13，13 |
| D、13，13.5 |
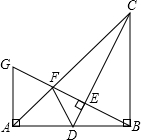如图，在Rt△ABC中，AB=BC，∠ABC=90°，点D是AB的中点，连接CD，过点B作BG⊥CD，分别交CD，CA于点E，F，与过点A且垂直于AB的直线相交于点G，连接DF，给出以下五个结论：①
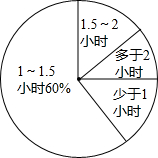为进一步规范教育教学行为，切实减轻学生的课业负担，某校想了解本校九年级学生家庭作业用时情况．