题目内容
在等腰△ABC中,∠ACB=90°,且AC=2,过点C作直线l∥AB,P为直线l上一点,且AP=AB,则点P到BC所在直线的距离是 .
考点:勾股定理,平行线之间的距离,含30度角的直角三角形,等腰直角三角形
专题:分类讨论
分析:如图1,延长AC,做PD⊥BC交点为D,PE⊥AC,交点为E,可得四边形CDPE是正方形,则CD=DP=PE=EC;等腰Rt△ABC中,∠C=90°,AC=2,所以,可求出AC=2,AB=2
,又因为AB=AP;所以,在直角△AEP中,可运用勾股定理求得DP的长即为点P到BC的距离.如图2,延长BC,作PD⊥BC,交点为D,延长CA,作PE⊥CA于点E,同理可证,四边形CDPE是正方形,同理可得,在直角△AEP中,可运用勾股定理求得DP的长即为点P到BC的距离.
| 2 |
解答: 解:①如图1,延长AC,做PD⊥BC交点为D,PE⊥AC,交点为E,
解:①如图1,延长AC,做PD⊥BC交点为D,PE⊥AC,交点为E,
∵CP∥AB,
∴∠PCD=∠CBA=45°,
∴四边形CDPE是正方形,
则CD=DP=PE=EC,
∵在等腰直角△ABC中,AC=BC=2,AB=AP,
∴AB=
=2
,
∴AP=2
;
∴在直角△AEP中,(2+EC)2+EP2=AP2
∴(2+DP)2+DP2=(2
)2,
解得DP=
-1;
 ②如图2,延长BC,作PD⊥BC,交点为D,延长CA,作PE⊥CA于点E,
②如图2,延长BC,作PD⊥BC,交点为D,延长CA,作PE⊥CA于点E,
同理可证,四边形CDPE是正方形,
∴CD=DP=PE=EC,
同理可得,在直角△AEP中,(EC-2)2+EP2=AP2,
∴(PD-2)2+PD2=(2
)2,
解得PD=
+1.
故点P到BC所在直线的距离是
-1或
+1.
故答案为:
-1或
+1.
 解:①如图1,延长AC,做PD⊥BC交点为D,PE⊥AC,交点为E,
解:①如图1,延长AC,做PD⊥BC交点为D,PE⊥AC,交点为E,∵CP∥AB,
∴∠PCD=∠CBA=45°,
∴四边形CDPE是正方形,
则CD=DP=PE=EC,
∵在等腰直角△ABC中,AC=BC=2,AB=AP,
∴AB=
| 22+2 |
| 2 |
∴AP=2
| 2 |
∴在直角△AEP中,(2+EC)2+EP2=AP2
∴(2+DP)2+DP2=(2
| 2 |
解得DP=
| 3 |
 ②如图2,延长BC,作PD⊥BC,交点为D,延长CA,作PE⊥CA于点E,
②如图2,延长BC,作PD⊥BC,交点为D,延长CA,作PE⊥CA于点E,同理可证,四边形CDPE是正方形,
∴CD=DP=PE=EC,
同理可得,在直角△AEP中,(EC-2)2+EP2=AP2,
∴(PD-2)2+PD2=(2
| 2 |
解得PD=
| 3 |
故点P到BC所在直线的距离是
| 3 |
| 3 |
故答案为:
| 3 |
| 3 |
点评:本题考查了勾股定理的运用,通过添加辅助线,可将问题转化到直角三角形中,利用勾股定理解答;考查了学生的空间想象能力.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
 如图,在等边△ABC中,AB=10,D是BC的中点,将△ABD绕点A旋转后得到△ACE,则线段DE的长度为
如图,在等边△ABC中,AB=10,D是BC的中点,将△ABD绕点A旋转后得到△ACE,则线段DE的长度为 如图,△ABC内接于⊙O,BC=12cm,∠A=60°.⊙O的直径为
如图,△ABC内接于⊙O,BC=12cm,∠A=60°.⊙O的直径为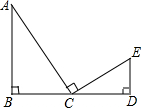 如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,∠A=30°,那么
如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,∠A=30°,那么 某校为了了解九年级500名学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起座的次数,并绘制成如图所示的频数分布直方图,请你根据图示计算,估计仰卧起座次数在15~20之间的学生有( )
某校为了了解九年级500名学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起座的次数,并绘制成如图所示的频数分布直方图,请你根据图示计算,估计仰卧起座次数在15~20之间的学生有( )